|
||||||||||||||||||||||||||||
Faites un double-clic pour un retour en haut de page
![]()
|
Nombres de MOTZKIN Nombres utilisés en
dénombrement, comme les nombres de Catalan.
Nommé ainsi d'après Théodore Motzkin. Applications en combinatoire et en théorie des nombres. |
|
|
|
|
Un nombre de Motzkin d'ordre
n est définit par la relation de
récurrence:
Soit les nombres de Motzkin pour n de 0 à 50. 1, 1, 2, 4, 9, 21, 51, 127, 323, 835, 2188, 5798, 15511,
41835, 113634, 310572, 853467, 2356779, 6536382, 18199284, 50852019,
142547559, 400763223, 1129760415, 3192727797, 9043402501, 25669818476,
73007772802, 208023278209, 593742784829, 1697385471211, 4859761676391,
13933569346707, 40002464776083, 114988706524270, 330931069469828, 953467954114363, 2750016719520991, 7939655757745265,
22944749046030949, 66368199913921497, 192137918101841817, 556704809728838604,
1614282136160911722, 4684478925507420069, 13603677110519480289,
39532221379621112004, 114956499435014161638, 334496473194459009429,
973899740488107474693, 2837208756709314025578
= 2,83 1021 = M50 En rouge
les trois nombres premiers
de Motzkin jusqu'à n = 10 000. |
|
|
|
||
|
Exemple simple de programmation avec liste et mise à jour
des paramètres par décalage.
|
Initialisation, y compris une liste L (1,1). Boucle en commençant par 2; les deux premières valeurs sont connues (1
et 1). Calcul de la valeur de M2 (en fait Mn) M2 est jouté à la liste existante L. Décalage d'un cran pour les deux valeurs précédentes. Fin de boucle (od) Impression de la liste L. Résultat de l'impression. |
|
Voir
Programmation
|
|
||
|
Règle du jeu Un insecte part du point 0
pour rejoindre le point M situé au même niveau et à une distance n. Son
parcours symbolise le nombre Mn. |
Les capacités de l'insecte sont
limitées. Il ne peut monter ou descendre que d'un cran à la fois. Mn est la
quantité de possibilités offertes à l'insecte. |
|
|
Illustration
Notation M2
= (hh), (md) M3
= (hhh), (hmd), (mdh), (mhd) M4
= (hhhh), (mdhh), (hmdh), (hhmd), (mhdh), (hmhd), (mhhd), (mdmd),
(mmdd). |
||
|
|
||
|
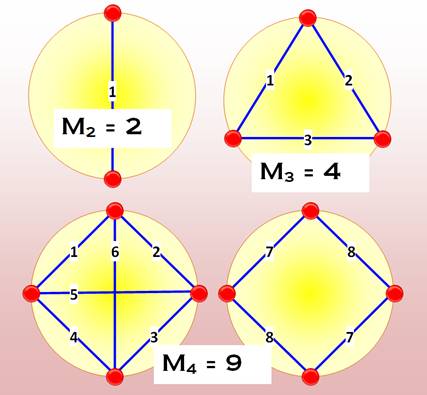
Manières de tracer des cordes entre n points sans qu'elles
se coupent ni se touchent. Dans le décompte, le cercle
sans corde compte pour 1. 2 points: 1 seule corde: M2 = 1 + 1 = 2 3 points: 3 cordes: M3 = 3 + 1 = 4 4 points: 6 cordes seules et 2 paires de cordes: M4 = 6 + 2 + 1 = 9 5 points: 10 cordes seules 5 paires courtes 5 paires mixtes M5 = 10 + 5 + 5 + 1
= 21 |
|
|
|
Note: le premier dessin de M5 aurait dû être
décomposé en dix dessins autonomes pour monter que les cordres 1, 2, 3 … ne
se coupent pas, et ne se touchent pas. Idem pour le premier dessin pour M4. |
||
Voir
Partage du cercle avec des cordes –
Cas général
|
|
||
|
Formule |
|
|
|
Catalan |
Somme du produit du coefficient
binomial et du nombre de Catalan. |
|
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
Cette page |
![]()