|
||||||||||||||||||||||||||
![]()
|
RÉGIONS
crées par n CERCLES Division du plan par des cercles Des cercles dessinés sur une feuille
partagent le plan en différentes régions. Combien au maximum pour n cercles? |
Voir Toutes les possibilités de partager le
cercle
Anglais: Draw n circles in the plane; what is the maximal
number of regions
into which the
plane is divided
|
|
||
|
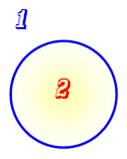
Avec un
seul cercle, le plan est partagé en deux zones: la zone intérieure et la zone
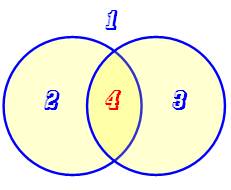
extérieure. Avec deux
cercles, le plan est partagé en quatre régions. Avec
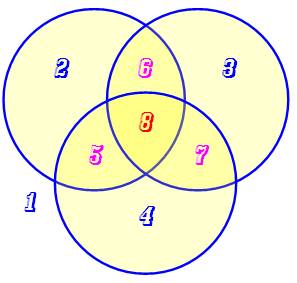
trois cercles, il y a huit régions. On compte:
On
propose la formule:
|
|
|
|
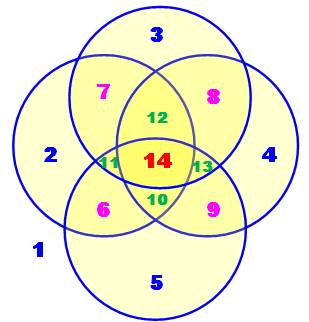
Avec
quatre cercles, on compte:
On
vérifie la formule proposée plus haut:
|
|
|
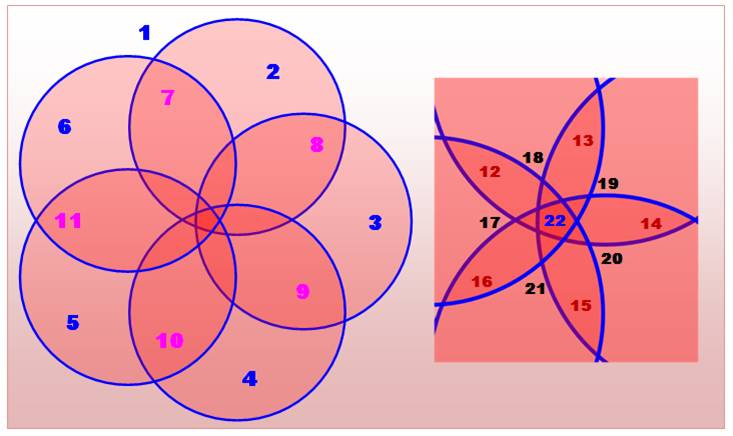
Cas de cinq cercles avec 22 régions
|
|
||
|
La
quantité de régions Q est bien donnée par la formule imaginée ci-dessus. |
Q = (n – 1) n + 2 = n² – n +
2 |
|
|
Liste de valeurs En rouge les valeurs vérifiées ci-dessus. Il
n'est pas très compliqué de prouver l'extrapolation ayant conduit à la
formule. |
2, 4, 8, 14, 22, 32, 44, 58, 74, 9210,
112, 13412,
158, 184, 212,
242,
274,
308,
344,
38220,
422,
464,
508,
554,
602,
652,
704, 758, 814,
87230,
932,
994,
1058, 1124, 1192, 1262, 1334, 1408, 1484, 1562, 1642, 1724, 1808, 1894, 1982,
2072, 2164, 2258, 2354, 2452, … |
|
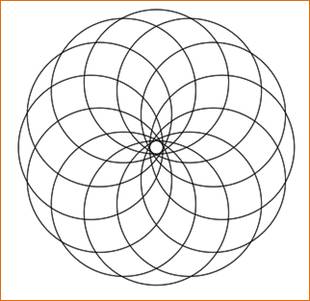
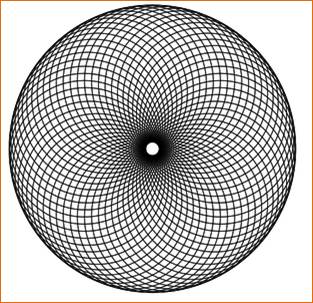
Cas de 12 cercles (134 régions) et de 60 cercles (3 542 régions)
Voir Brève
511
Construction des 12 cercles avec Geogebra

|
|
|||
|
La
quantité de régions Q créées par n sphères qui se coupent dans l'espace |
Q = 1/3 n (n² – 3n + 8) |
||
|
Liste de valeurs |
2, 4, 8, 16, 30, 52, 84, 128, 186, 260, 352, 464, 598, 756, 940, 1152,
1394, 1668, 1976, 2320, 2702, 3124, 3588, 4096, 4650, 5252, 5904, 6608, 7366,
8180, 9052, 9984, 10978, … |
||
![]()
|
Retour |
|
|
Voir |
|
|
|
|
|
Cette page |
![]()