|
Édition du: 29/12/2024 |
|
INDEX |
QUADRILATÈRES – Compter |
||
|
|
|||
Faites
un double-clic pour un retour en haut de
page
![]()
|
Quantité de CARRÉS dans le CERCLE
Il existe une variété de problèmes concernant la
quantité de carrés recouvrant un cercle:
|
||
|
|
Sommaire de cette page >>> Combien de carrés
dans un cercle >>> Cas du carré
inscrit dans le cercle >>> Problème de Gauss >>> Maximum de carrés en
vrac |
Débutants Glossaire |
|
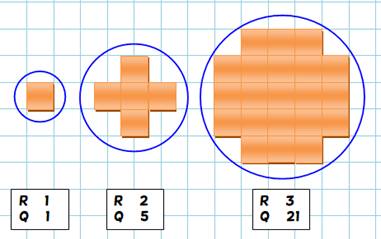
Plus grand carré dans le cercle Nous
cherchons à inclure une quantité maximale (Q) de carrés unités dans un cercle
de rayon R donné en nombres entiers. Trois
cas se présentent (détaillés
ci-dessous):
Note Un
autre problème consiste à compter les carrés alignés d'une figure polygonale
recouvrant le cercle tout en chevauchant la circonférence. |
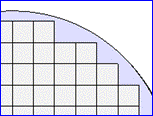
Cas de cafféq alignés internes au cercle
Cas des carrés chevauchant la circonférence R
= 3 => Q = 24
|
|
|
Nombres entiers Assembler
les carrés unité en un grand carré et l'inscrire dans un carré revient à
s'intéresser au carré inscrit dans un cercle. Ici,
nous souhaitons que le diamètre soit un nombre entier. La
diagonale du carré est alors égale au diamètre du cercle: D = C√2. Dans
le cas de n = 3 et Q = n² = 9, on a: D = 4,24… et, le nombre entier
immédiatement supérieur est 5. Liste
des valeurs du diamètre entier pour n de 1
à 25: En
imposant un rayon entier, la valeur du
diamètre sera un nombre pair et deviendra: |
Cas du carré inclus R
= 5 => Q = 9
|
|
Comparaison des
diamètres pour diamètre entier ou rayon entier (diamètre pair)

|
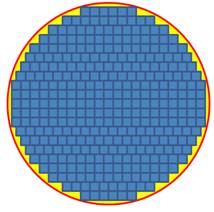
Maximum de carrés alignés ou problème de Gauss C'est
le cas le plus étudié. Le
centre du cercle est au centre du carré central. La
quantité maximale de carrés unités alignés inclus dans un cercle de rayon à
partir de 1 est: |
Cas du maximum de carrés unités alignés
|
|
Voir Gauss
|
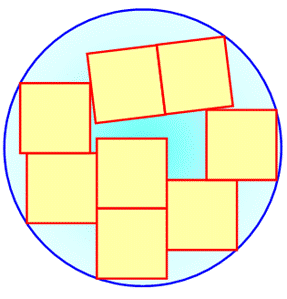
Maximum de carrés en position quelconque Dans
ce cas, on cherche plutôt le rayon du cercle
le plus petit contentant n carrés unités. Le rayon étant exprimé par
un nombre réel (en non pas entier). Ces
cas sont listés et illustrés pour n de 1 à 35 dans l'article Squares in Circles
d'Erich Friedman Par exemple Voir liste ci-dessous |
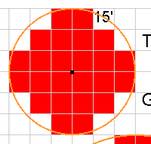
Cas du maximum de carrés unités en vrac Q
= 8 => R = 1,978…
|
|
Rayon minimum des
cercles contenant de 1 à 10 carrés unités
n nombre de carrés dans le cercle de
rayon R; Ce/Ca: rapport des aires entre cercle et carrés

Voir Nombre
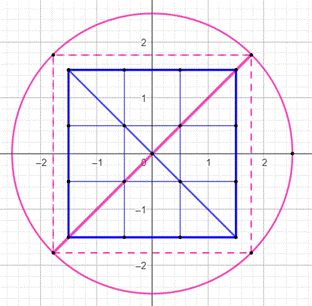
2,121…
Cas de n = 9
Le cercle passe exactement par les
quatre points rouges
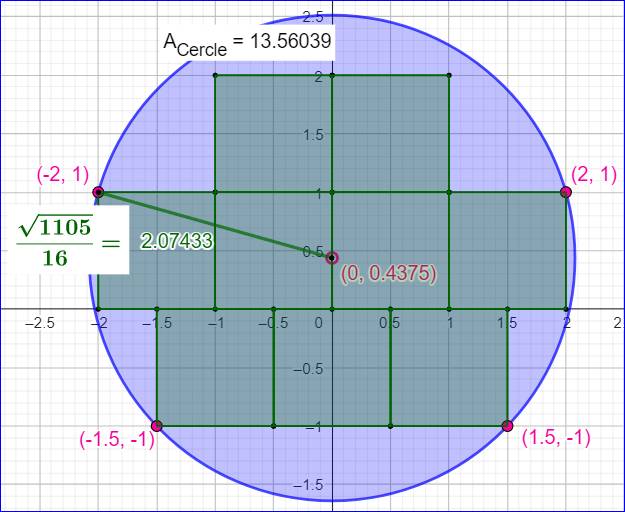
L'aire bleue (4,560…) est proche de la
moitié de celle des carrés verts (9)
![]()
|
Suite |
|
|
|
Voir |
|
|
|
Site |
|
|
|
Cette page |
||
![]()