|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
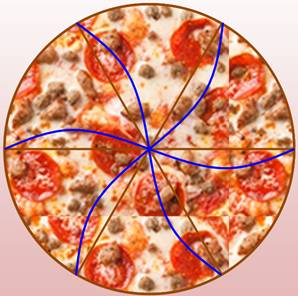
Pavage du DISQUE ou de la PIZZA Comment partager une pizza de sorte que certaines parts ne comportent pas de part centrale. |
|
|
||
|
Découpe
classique en douze parts et découpe ondulée. Toutes les parts partent du
centre. Et, si
certaines personnes n'aimaient que les zones périphériques ? Comment alors découper
la pizza tout en formant des parts égales. Note: Pour une tarte, la bordure est souvent appelée le trottoir. |
||
|
Découpe
à 12 parts de "tarte" |
Découpe
ondulée à 6 parts |
|
|
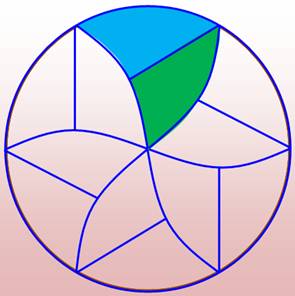
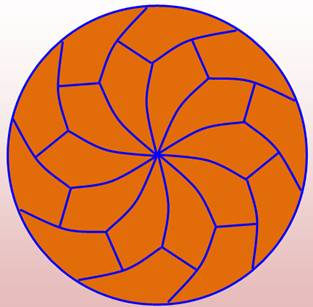
Avec un
segment droit supplémentaire, la pizza est découpée en douze parts identiques
dont la moitié ne donne que des morceaux de la périphérie. Les parts partant
du centre forment une rosace. La même chose à droite, avec découpe courbe de
même courbure que le cercle. |
||
|
Découpe
à 12 parts avec
parts non-centrales |
Découpe
à 12 parts courbes avec
parts non-centrales |
|
|
Bilan Ces
pavages à parts égales du disque sont connus depuis longtemps. Avec la même
méthode pour 6+6, il est possible d'obtenir une découpe 12+12, ou 6n+6n. Ou encore des panachés comme 4+8. Etc. |
||
|
|
|||
|
Pavage du
disque |
Hadley et
Worsley (décembre 2015 – université de
Liverpool) se pose la question de la découpe monohédrale du disque telle
qu'une partie au moins ne soit pas centrale. Ils ont démontré
que le pavage est possible quel que soit le Travaux,
évidemment sans intérêt pour les pizzas. La découpe de la pizza est une image
parlante. Car, ce résultat est une avancée dans le domaine du pavage des
surfaces. |
||
|
Pavage
monohédral Monohedral
tiling |
Découpe d'une
surface plane en parties congruences (égales). |
||
|
Courbure |
Dans la découpe
centrale, il est nécessaire de retrouver des bordures courbes de même
courbure que le cercle. |
||
|
Exemple |
Au départ
une rosace à 12 pétales dont la courbure est exactement celle du cercle. Elle
est interne au cercle initial. Les
prolongements courbes et droits forment les douze parts supplémentaires. |
||
|
Les
auteurs construisent ce pavage en partant du pavage du plan par des tuiles
issues de polygones réfléchis. Ils
passent au cercle par courbure des tuiles en respectant les axes de symétrie. Voir image
ci-dessous et leur publication en anglais |
|
||
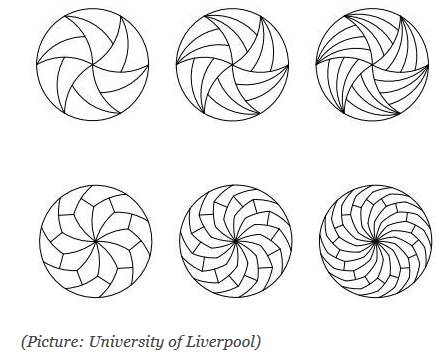
Extrait de la presse Américaine du 11 janvier 2016
|
|
||
|
Most of us divide a pizza using straight cuts that all meet in the
middle. But what if the centre of the pizza has a topping that some people
would rather avoid, while others desperately want crust for dipping? Mathematicians had previously come
up with a recipe for slicing – formally known as a monohedral disc tiling
– that gives you 12 identically shaped pieces, six of which form a star
extending out from the centre, while the other six divide up the crusty
remainder. |
La plupart
d'entre-nous partage la pizza en faisant des coupes droites qui se rejoignent
toutes au centre. Et si, au centre de la pizza, se trouvait une garniture que
certains voudraient plutôt éviter, alors que d'autres insisteraient pour
avoir la croûte en guise de mouillette? Les
mathématiciens avaient déjà trouvé une méthode de partage – officiellement
connue sous le nom de pavage monohédral du disque – qui vous donne douze
parts identiques, dont six forment une étoile partant du centre, alors que
six autres divisent la partie croustillante restante. |
|
![]()
|
Suite |
|
|
Voir |
|
|
|
|
|
DicoNombre |
|
|
Cette page |
![]()