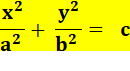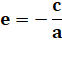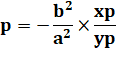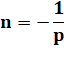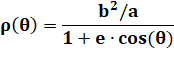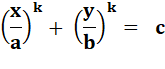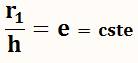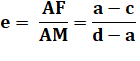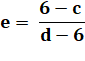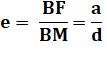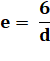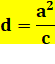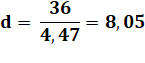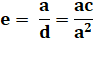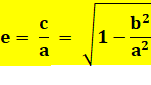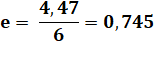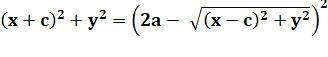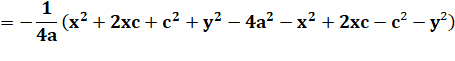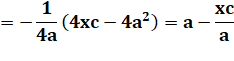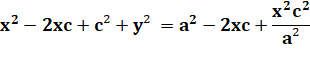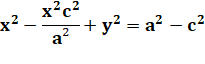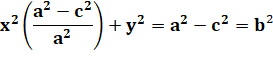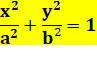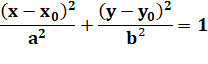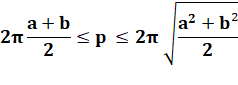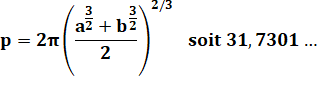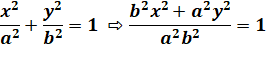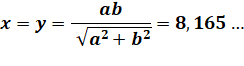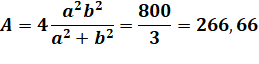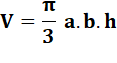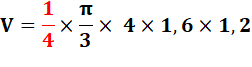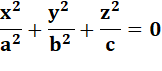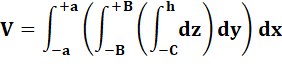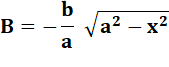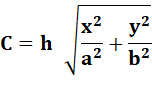Ellipse

NOMBRES - Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 07/10/2024 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Géométries
Débutants Géométrie	CONIQUES				Glossaire Géométrie
INDEX Courbes Géométrie	Coniques	Ellipse	Hyperbole	Parabole
	Cercle	Son périmètre	Ovale	Segment de Parabole
		Propriétés diverses		Quart d'ellipse
		Sommaire de cette page >>> Construire le centre, les axes et les foyers >>> Ellipse et ovale >>> Ellipse – Faits >>> Allure >>> Équations - Résumé >>> Super ellipse >>> Ellipse en chiffres >>> Aire et périmètre de l'ellipse >>> Rectangle inscrit dans l'ellipse >>> Volume du cône elliptique

ELLIPSE

L'ellipse est l'une des trois coniques. Un cercle aplati qui partage de nombreuses similitudes mathématiques avec lui, mais qui s'évade vite vers la complexité de calcul.

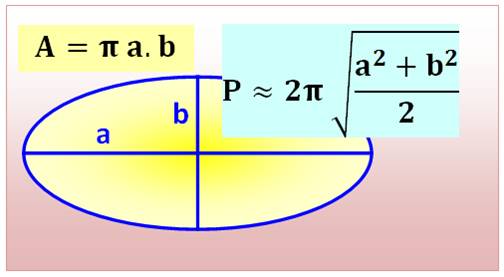
La trajectoire des planètes autour de leur étoile est une ellipse. Les trois lois de Kepler modélisent leur orbite.

Aire et périmètre de l'ellipse en fonction du grand axe et du petit axe

Développements >>>

A) Construire (règle et compas) le centre de l'ellipse connaissant son tracé

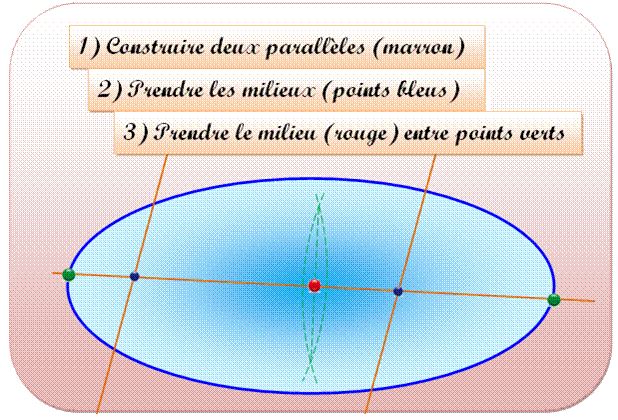
En vert pointillé: construction de la médiatrice.

Voir Centre du cercle / Constructions élémentaires

B) Construire les deux axes connaissant le centre

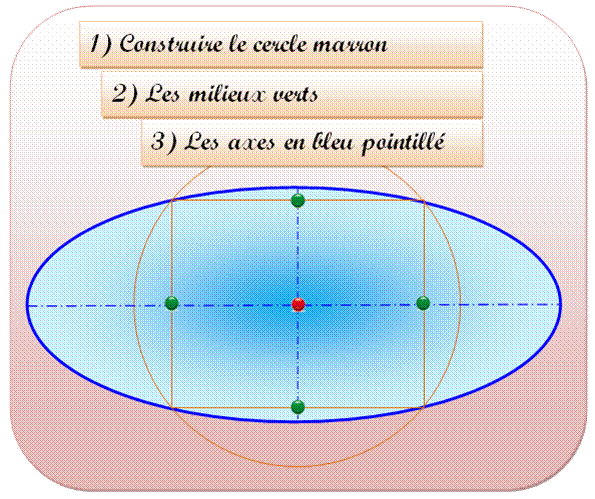
C) Construire les deux foyers de l'ellipse connaissant les deux axes

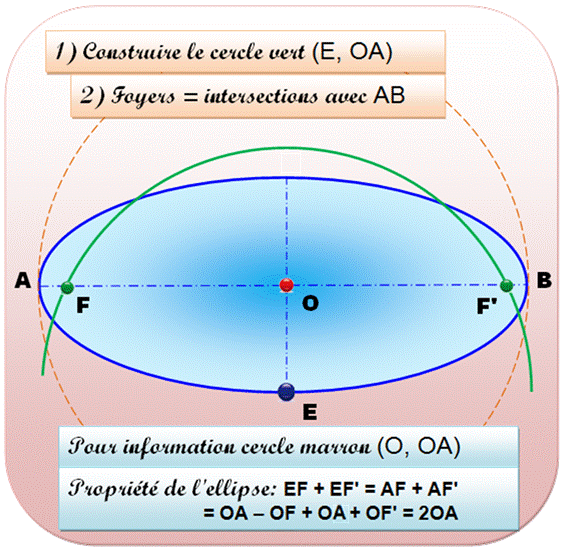
Voir Autres constructions avec l'ellipse / Constructions géométriques – Index

Merci à Patrick Herrmann pour sa relecture attentive

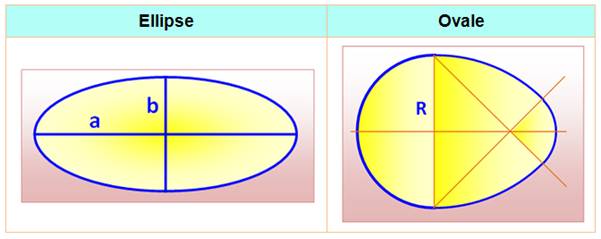
ELLIPSE et OVALE
ELLIPSE Étymologie: une ellipse du grec elleipsis, manque, défectueux. Courbe plane dont tous les points sont tels que la somme de leur distance à deux points fixes appelés foyers est constante. Aussi: Sous-entendu, raccourci dans l'expression de la pensée.	OVALE Ovale du latin ovum, œuf. Courbe plane, fermée, convexe et allongée, ayant deux axes de symétrie comme l'ellipse.

Voir Ovale / Historique avec Dürer et Kepler

ELLIPSE – FAITS

C'est une sorte de cercle vu de travers, en perspective.

On rencontre l'ellipse en sectionnant un cône.

C'est la courbe du jardinier : Prendre une ficelle fixée à deux piquets en M et M'. Un plantoir en M décrira une ellipse en gardant la ficelle tendue.

Voir Cercle et ellipse du jardinier

La trajectoire des planètes et des comètes est une ellipse dont le Soleil est l'un des foyers; découverte faite par Kepler en 1609.

Voir Spirale du jardinier / Équerre du jardinier / Construction de l'ellipse

ALLURE

Courbe telle que:

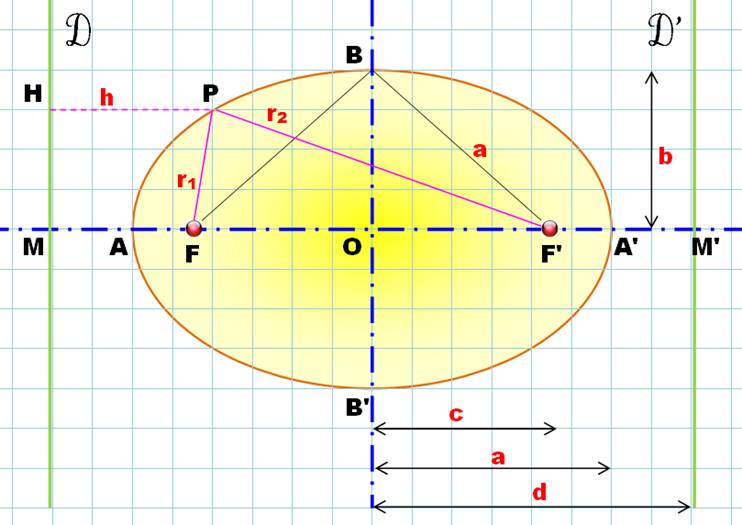
MA + MB = 2a

Son équation:

Voir Explications

Forme de l'ellipse:

- Effet de l'un des paramètres a et b:

a vaut successivement: 1 (cercle), puis 2, 3, 4 et 5;

tandis que b reste égal à 1 (et c vaut 1).

- Effet de la constante c:

a et b sont constants: a = 2 et b = 1;

c vaut successivement: 1 , 2 , 4 , 8 et 16.

Équations - Résumé

Équation cartésienne de l'ellipse centrée en E (c, d) et demi-axes a et b
Demi-distance focale: OF = OF' = c
Point P sur l'ellipse	PF + PF' = 2a
Excentricité
Pente de la tangente en P(xp, yp)
Pente de la normale en P(xp, yp) Voir Application
Tangente passant un point M (xm, ym) extérieur à l'ellipse. Les pentes p sont solutions de l'équation:	(a² – xm)p² + 2·xm·ym·p + (b² – ym²) = 0
Équations paramétriques Axes parallèles aux axes du repère	x = a cos(t) y = b sin (t)
Axes obliques aux axes du repère	x = a cos(t) y = b sin (t + φ)
Équation polaire

Super ellipse

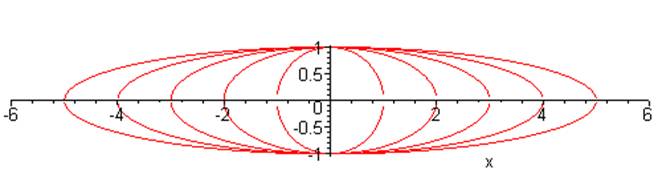
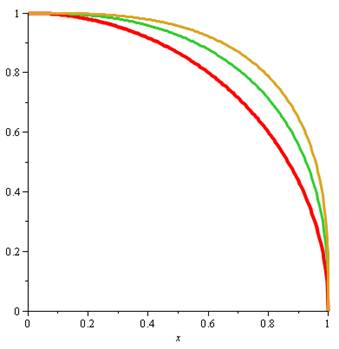
Une ellipse gonflée ou ovale.

En rouge k = 2 (ellipse)

En vert k = 2,5, et

En jaune k = 3.

Voir Équation des formes ovales

Ellipse en chiffres
L'ellipse est le lieu des points P tels que => C'est aussi le lieu des points tels que => La constante e est l'excentricité. Pour l'ellipse: 0 < e < 1.

Opération	Formulation	Exemple numérique
Segments BF et BF'	BF + BF' = 2a BF = BF' = a	BF = a = 6
Distance au foyer c	c² = a² – b²	c² = 36 – 16 = 20 c = 4, 47
Excentricité au point A
Excentricité au point B
Résolution de ces deux équations en d
Valeur de l'excentricité

Équation cartésienne de l'ellipse
Valeurs de r₁ et de r₂
Relation pour l'ellipse
Au carré
Valeur sous radical
Au carré
En divisant
Si le centre est en O (x₀, y₀)
Équation générique		Ax² + By² + Cx + Dy + E = 0
Équation paramétrique

Périmètre de l'ellipse ou circonférence de l'ellipse

Paramètres de l'ellipse

Encadrement du périmètre (et exemple avec a = 6 et b = 4)

Méthode des cercles équivalents de circonférence

Kepler (1571-1630) utilisait un cercle équivalent tel que:

En 1883, Thomas Muir (1844-1934) donne cette formule qui améliore nettement le résultat:

Formules plus précises et explications sur le périmètre de l'ellipse >>>

Rectangle inscrit dans l'ellipse
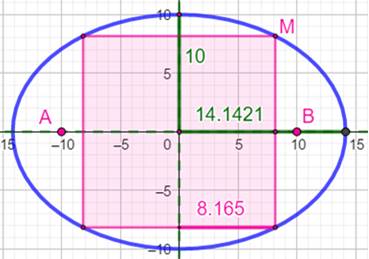
Soit une ellipse avec ses foyers en (-10, +10) et ses demi-axes . Comment construire le carré inscriptible dans l'ellipse ? Par le calcul du côté du carré.
Ellipse Son équation: Aire de l'ellipse	Côté du carré Le point M à la fois sur l'ellipse et sommet du carré est tel que x = y Aire du carré (= 4 x²)

Cône elliptique
Le volume d'un cône droit de base elliptique est égal à: Voir Volume du cône / Cône elliptique – Développements
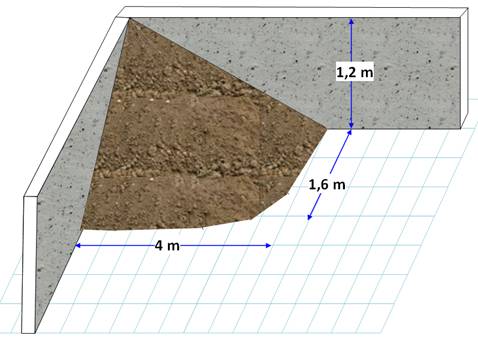
Exemple Un tas de terre se trouve dans l'angle d'un mur rectangulaire. Cette terre ayant été déversée depuis l'angle supérieur du coin des deux murs, elle s'est répandue assez régulièrement en un tas de forme plus ou moins conique.
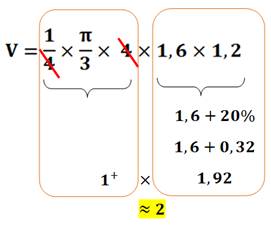
		Calcul de tête
Calcul de la formule Équation du cône avec origine au sommet. Pour
Volume du cône Le calcul de cette intégrale triple avec ces paramètres (pas simple) donne bien la formule indiquée.

Anglais: how to find the volume for a right elliptical cone?

Demi-grand axe et demi-petit axe: semi major axis and semi minor axis

Anecdote suite à une pluie torrentielle survenue en janvier 2014

J'ai eu à effectuer ce calcul de volume suite à un éboulement de terre de 40 m³ en provenance de la propriété voisine située au-dessus de la mienne. La majorité de cette terre s'est déversée dans le coin muré de mon jardin.

Suite	Calcul du périmètre de l'ellipse Cercle inscrit dans le quart d'ellipse Cône elliptique – Développements Constructions de l'ellipse Construction de l'ellipse inscrite dans un triangle Ellipse – Curiosités, énigmes Ellipse dorée Fonctions elliptiques Hexagone mystique de Pascal Hyperbole Lois de Kepler – Orbite elliptique des planètes Ovale – Ove Point de Frégier Théorème de Brianchon Théorème de Pascal
Voir	Centre de gravité de l'ellipse Cercle Cône Courbes élémentaires Courbes elliptiques DicoMot Géométrie – Débutants Géométrie – Glossaire Géométrie – Index Lois de Kepler Parabole Sphère Théorème de Pascal
Sites	La géométrie de l'ellipse – GFA-BASIC 32 Codes Ellipse – Wikipédia Ellipsographe – Wikipédia – Voir Animations Ellipse (Mathcurve) – Robert FERRÉOL, Jacques MANDONNET, Alain Esculier Ellipse – Physique et simulations numériques Les coniques – Serge MEHL Les coniques – Applets par XiTi Les coniques – Bibm@th Les coniques – M@ths et tiques Perimeter of an ellipse – Gilles Cazelais – Justification de la formule itérative 1 donnée ci-dessus. Approximations of Ellipse Perimeters – Review of known formulae – Stanislas Sykora – 2005 - Toutes les formules connues et leurs comparaisons Ellipse Perimeter – The quest for a simple, exact expression - document pdf de 74 pages
Cette page	http://villemin.gerard.free.fr/Geometri/Coniques/Ellipse.htm