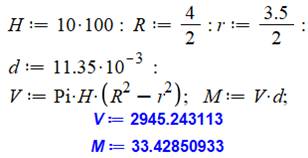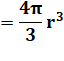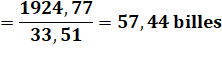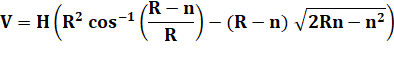|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
CYLINDRE Propriétés, problèmes,
curiosités et amusements. Nous aborderons d'abord le
cylindre classique de révolution et généraliserons ensuite. Cylindre vient du grec kulindros,
le tambour. Le cylindre désigne aussi bien le volume que la surface. Il n'y a
pas de mot distinguant le solide cylindre et la surface cylindrique. |

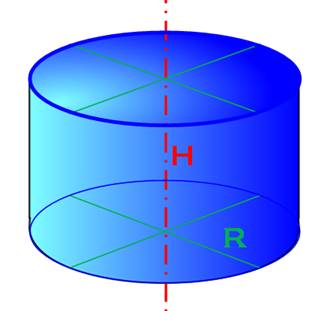
Cylindre
de serrure

|
|
||
|
Le vocabulaire et propriétés du cylindre
|
Cylindre classique appelé cylindre de révolution ou encore cylindre circulaire droit.
|
|
|
|
|
Voir Mnémotechnique / Découpe de la Pizza
|
|
||
|
|
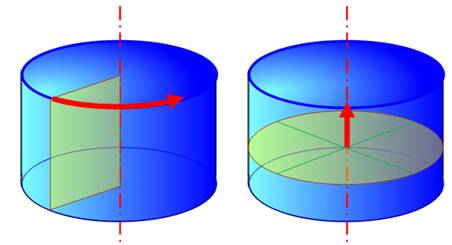
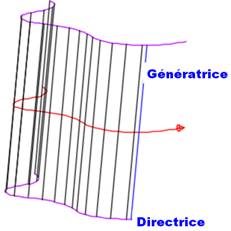
Deux méthodes pour engendrer un cylindre. |
|
Voir Tour de Hanoï
|
|
||
|
|
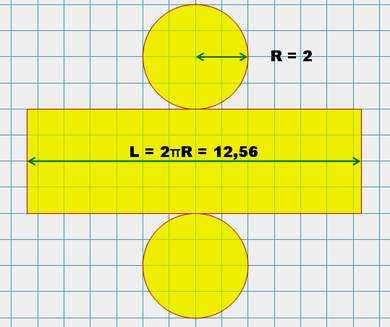
Unité = côté du carré du quadrillage. |
|
Voir Patron du
cube
|
|
|||
|
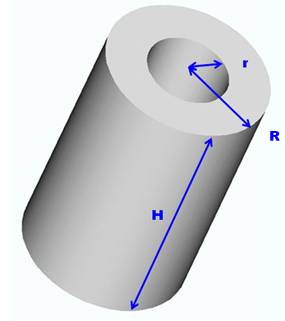
Le volume du cylindre creux
(un tuyau, par exemple):
|
|
||
|
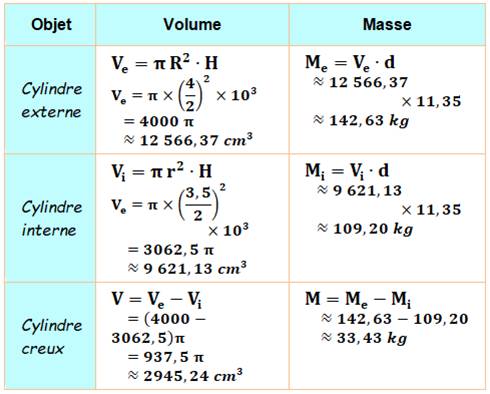
Exemple numérique Un tube
de 10 mètres de long en plomb (densité 11,35 g.cm-3). Diamètre
extérieur 4 cm et intérieur 3,5 cm. Quelle
est la masse de ce tuyau? Réponse: Ordre de grandeur Le volume du cylindre ne dépasse celui d'une
barre à base carrée. Son volume: 4x4x1000 = 16 000 cm3 |
|
||
|
Calcul avec logiciel en appliquant directement la formule |
|
||
Merci à Frédérique Olivari pour ses corrections
nécessaires !
|
|
|||
|
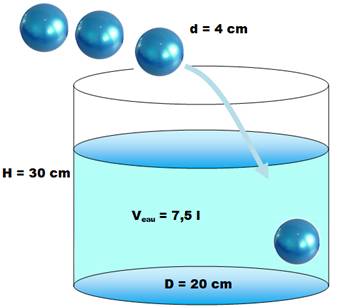
Il y a déjà 7,5 litres d'eau
dans la cuve.
|
|
||
|
|
Vcylindre |
|
|
|
|
Vsans eau |
|
|
|
|
VBille |
|
|
|
|
Q |
|
|
|
|
|
la 57e, un numéro impair. |
|
|
|
|
La 58e, un numéro pair. |
|
|
C'est Alexis qui place la première bille
(impaire) et Chloé qui place la deuxième (paire). C'est donc Chloé qui fait déborder la cuve en
mettant la 58e (paire). |
|||
Le cylindre idéal?
|
Même
volume: aire minimale pour H = 2R = D. Même
aire: volume maximum pour H = 2R = D. Ce
cylindre particulier avec H = D est donc contenu dans un cube. |
Voir Cylindre, sablier et sphère – Comparaison
|
|
|||
|
|
|
||
|
Principaux types de cylindres
"réguliers" |
Droit
Oblique
Elliptique (droit)
Right Oblique Elliptical (right) |
||
|
|
|||
|
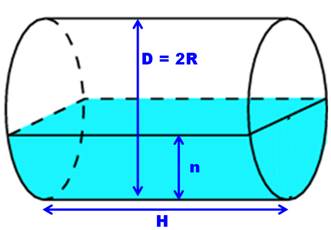
Une cuve cylindrique posée
horizontalement contient un liquide jusqu'au niveau n. Comment calculer le volume
de liquide?
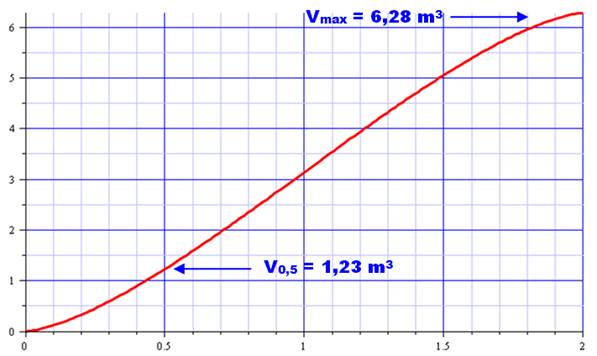
Note: Cos-1
est équivalent à arccos, fonction qui donne l'angle lorsqu'on connait le cosinus Exemple: H = 2 m; R = 1
m; n = 0,5 m (R – n) / R = 0,5 Angle: arccos(0,5) = 1,047 2Rn – n² = 2x1x0,5 – 0,25 =
0,75 = 0,866² V = 2 (1² x 1,047 – 0,5 x
0,866) = 1,228 m3 |
|
||
|
Volume de liquide dans la cuve selon en fonction
du niveau n. Avec H = 2 et R = 1. |
|
||
Voir Segment de cercle / Tonneau
|
|
||
|
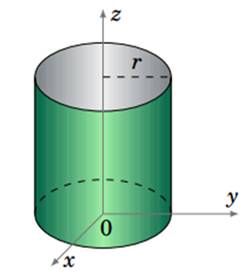
Les points de la surface
cylindrique sont tous à égale distance de l'axe. |
|
|
|
Avec ce système d'axes (figure),
l'équation de la surface cylindrique est: x² + y² = r² pour tout z de 0 à H. |
|
|
|
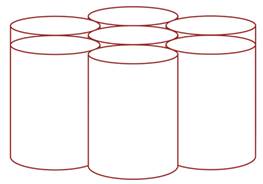
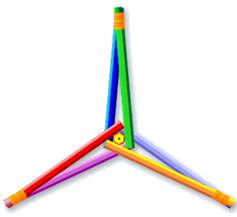
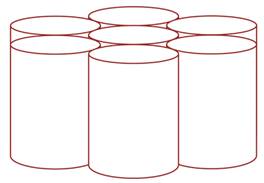
Il
est possible de positionner sept cylindres de façon telle que chacun soit
tangent aux six autres.
Cas avec trois
cylindres tangents
Solution avec six cylindres qui se touchent
Solution
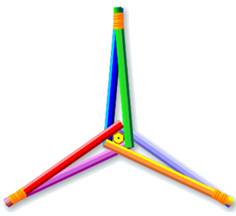
avec sept cylindres infinis, chacun est tangent aux six autres. Problème
abordé par Martin Gardner dans la revue Scientific American: pouvez-vous
disposer sept cigarettes telles que chacune touche les six autres? Gardner
donne la solution illustrée ici avec des crayons. En
2014, Sandor Bozoki, Académie hongroise des sciences, trouve une solution où
tous les cylindres se touchent par leur partie latérale et non pas les bouts.
Autrement-dit, il s'agit de sept tubes de longueur infinie. Le problème a été
résolu par ordinateur. Aucune maquette n'est assez précise pour restituer
l'exactitude des tangences. |
Source: A tale of
touching tubes /

|
|
|
|
|
|
|
Cylindre oblique - Page spéciale >>> |
|
![]()
|
CYLINDRE
- Index |
|
|
Aussi |
|
|
DicoNombre |
|
|
Sites |
|
|
Cette page |
![]()