NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 13/07/2023 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	CERCLE
Débutants Géométrie	CERCLES INSCRITS …				Glossaire Géométrie
INDEX Cercles Triangles	Index	Inscrit	SANGAKUS	Deux cercles – Triangle
	Introduction	Inscrit (suite)	Jumeaux	Deux cercles – Carré
	Puissance	Circonscrit	Carré max	Deux cercles – Carré et triangle
		Exinscrits	Face à face	Trois cercles – Construction
				Trois cercles – Tr. Équilatéraux
		Théorème des six cercles		Quatre cercles – Construction
		Sommaire de cette page >>> Théorème des six cercles >>> Théorème des six (ou quatre) cercles de Miquel

Théorème des six cercles

haut

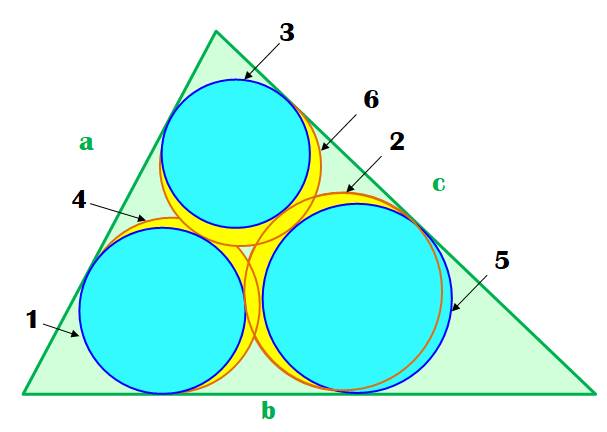
Construction

Un triangle quelconque.

Trois cercles inscrits dans chacun des angles

Trois nouveaux cercles inscrits dans chacun des angles ET tangent à un des cercles précédents.

Peut-on poursuivre la construction ? Non ! Le nouveau cercle prend la place d'un cercle existant déjà.

Cercles	C1	C2	C3	C4	C5	C6
Tangences	a, b	b, c, C1	c, a, C2	a, b, C3	b, c, C4	c, a, C5

Théorème des six cercles

Avec cette construction, C₆ est aussi tangent à C₁.

Chaque cercle est tangent quatre fois: à deux côtés et à deux cercles.

Condition

Pour lever l'ambiguïté entre deux choix, la tangence est choisie de sorte le centre de chaque cercle soit le plus proche du sommet de l'angle de tangence.

Généralisation

Propriété valable pour tout polygone à n côtés. Le cycle est alors égal à 2n étapes si n est impair et n étapes si n est pair.

Contexte

Théorème publié en 1974 par les Anglais John Evelyn, Godfrey Money-Court et John Tyrrell.

Théorème des six cercles de Miquel			haut
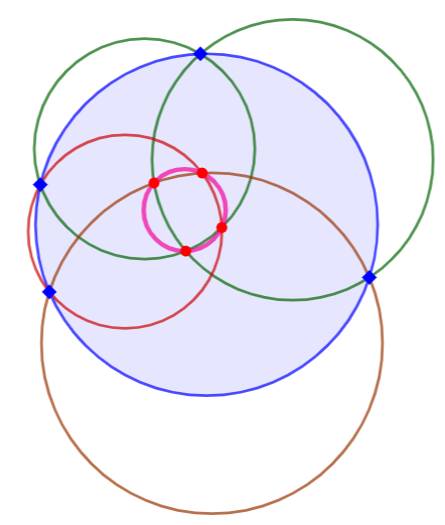
Construction Un cercle (bleu). Un cercle quelconque sécant (vert). Un nouveau cercle sécant passant par un des points d'intersection précédent. Un troisième cercle sécant passant par un des points d'intersection précédent. Un quatrième cercle sécant et passant, cette fois, par deux points d'intersection. Bilan: quatre cercles sécants quelconques, chacun passant par les points d'intersection de ses voisins. Théorème: les quatre points d'intersection centraux sont cocycliques, créant un sixième cercle ayant les mêmes propriétés d'intersection que le premier cercle.
Contexte	Connu sous le nom du théorème des quatre cercles de Miquel ou des six cercles de Miquel (Miquel's six circle theorem or six circle theorem or four circle theorem. Sans nul doute connu de Jakob Steiner 1796-1863), la seule preuve connue est due à Auguste Miquel (1816-1851).

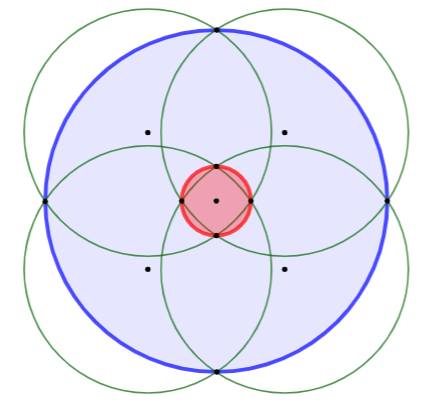
Exemple pour quatre cercles (verts) de même diamètre

dont les centres sont situés au sommet d'un carré.

Suite	Arbelos Carré et deux cercles tangents Cercle inscrit Chaine de Pappus Miquel – Théorème des trois cercles	Puissance d'un point par rapport à un cercle Quatre cercles Rayon du cercle circonscrit Sangakus
Voir	Bissectrices Cercle – Index Cercles et triangles Cône	Diamètre Géométrie – Vocabulaire Périmètre Sphère
Sites	Théorème des six cercles – Wikipédia Théorème de Miquel – Wikipédia Théorème des 2,3,4,5,6 cercles! – Bibm@th.net Benoit Chanceaux, Clara Feurtet, Enki Souillot, Olivier Couture, Frédéric Metin, et al.. La symphonie des cercles circonscrits. 2023. hal-03938043 Six circles theorem – Wolfram MathWorld – Animation The Six-Circles Theorem – Theorem of the day – Robin Whitty
Cette page	http://villemin.gerard.free.fr/GeomLAV/Cercle/SixCercl.htm