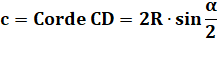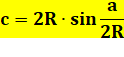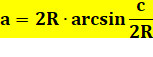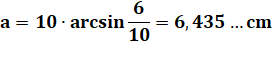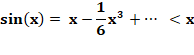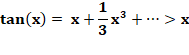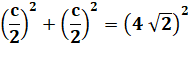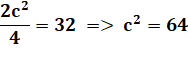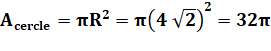NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 31/03/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	CERCLE
Débutants Géométrie	Propriétés				Glossaire Géométrie
INDEX Cercle	Cercle	Fondements	Équations	Théorèmes
	Centre	Propriétés	Angles	Partage
	Vocabulaire	Sécante	Tangente
	Cousines =>	Spirale	Hélice
		Sommaire de cette page >>> Périmètre & surface >>> Longueur de la corde >>> Arc et corde >>> Étude carré dans cercle >>> Périmètre des polygones >>> Pythagore dans le cercle >>> Corde et deux cercles >>> Relations typiques dans le cercle

Voir Fondements pour les propriétés fondamentales, de base

PÉRIMÈTRE & SURFACE (Aire)
Chaque formule utilise R, Pi et 2. Mais, le deux est placé différemment. Il est facile de se souvenir que le 2 indiquant le carré est utilisé pour l'aire. En effet, une aire est le produit de deux longueurs (l'aire se mesure en m²).	P: périmètre; R: rayon; A: aire. Il est extraordinaire d'avoir le même rapport: = P / 2R = A / R²
De toutes les figures planes de périmètre donné, le cercle est la figure qui offre la plus grande aire. Démonstration de Steiner

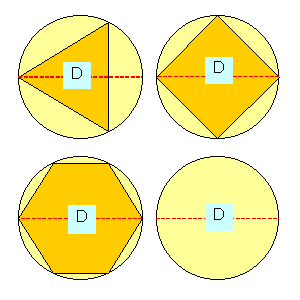
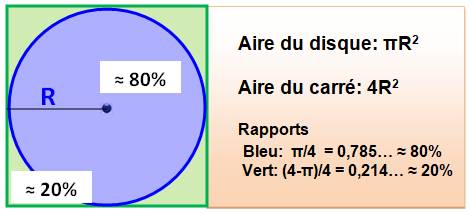
Proportions entre carré et disque

Longueurs et CORDE
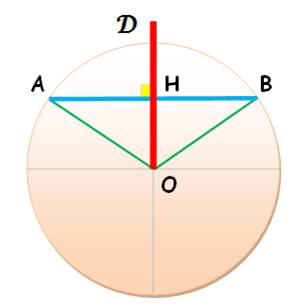
On donne le rayon du cercle R = 5 cm et la corde AB = 8 cm, calculez la distance du centre à la corde OH. Quelle est l'aire du triangle OAB? Le théorème de Pythagore nous dit que: OH² + AH² = OA² OH² = OA² – A H² = R² – (AB/2)² = 5² – 4² = 9 = 3² OH = 3 cm Aire du triangle OAB A = ½ AB x OH = ½ 8 x 3 = 12 cm²	Voir Démonstration sur la corde et sa médiatrice Dans le cas ou la corde est égale au rayon – le triangle OAB est équilatéral – on calcule avec la même méthode que OH = 3/2 R
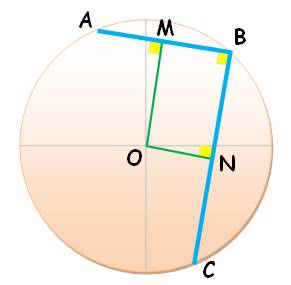
On donne deux segments AB et BC perpendiculaires mesurant 6 cm et 8 cm. Trouvez le rayon du cercle qui passe par les trois points. On trace les médiatrices OM à AB et ON à BC. Le point d'intersection O, avec OA = OB = OC, est le centre du cercle cherché. Le quadrilatère MBNO, avec ses trois angles droits est un rectangle. OM = NB = BC / 2 = 4 cm Avec Pythagore, à nouveau: R² = OB² = OM² + MB² R² = 4² + 3² = 25 = 5² R = 5 cm	Voir Démonstration sur les trois points et le cercle

ARC et CORDE
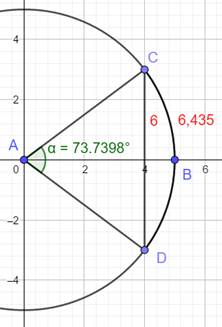
Relations Entre la longueur de l'arc et longueur de la corde. Exemple R = 5 cm et c = 6 cm
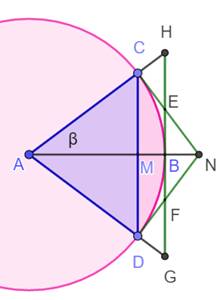
Relations avec la tangente (cercle de rayon unité) CM < Arc CB < HB = CN Le dévelopement en série prouve également cette relation:

Voir Trigonométrie / Limite de sin x

Étude carré dans cercle
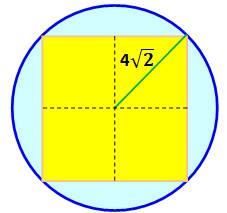
Énoncé Carré inscrit dans un cercle. Aire de la surface bleue ? Côté du carré Avec Pythagore: Aires

PÉRIMÈTRE DES POLYGONES
Les aires successives de ces polygones en fonction du diamètre sont: La limite du périmètre d'un polygone de " diamètre " D et ayant une infinité de côté est:	Voir méthode des polygones Voir Périmètre et paradoxes

PYTHAGORE DANS LE CERCLE
Devineriez-vous que les deux surfaces colorées ont la même aire? Les cercles concentriques pour rayons: 1, 2, 3, 4, 5. Aire du cercle rose: Aire de la couronne bleue: Nous trouvons là un triplet de Pythagore. 3² + 4² = 5² Les deux aires sont égales.	Aire bleue = Aire rose

Corde et deux cercles
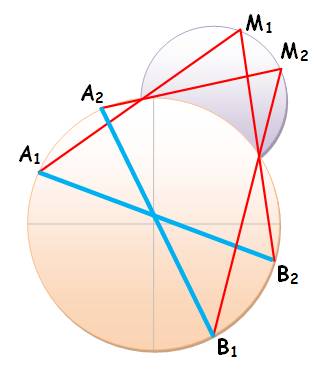
M est positionné n'importe où sur la circonférence d'un deuxième cercle. Les sécantes MA et MB passent pas les deux intersections des cercles. La corde AB a une longueur constante.	AB = constante

Relations typiques dans le cercle

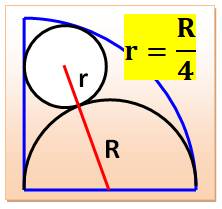
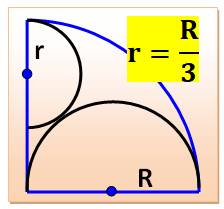
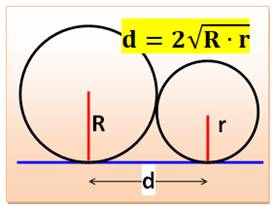
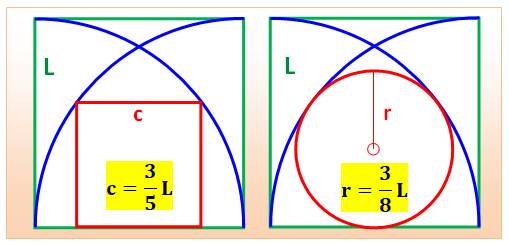
Voir Brève 55-1089 / Quarts de cercles / Défis en géométrie

English corner
A circle is symmetrical about any diameter. The straight line which bisects a chord at right angles passes through the center. One circle, and only one, can pass through any three points not in the same straight line.

Suite	Cercle – Équations Cercle – Fondements Cercles orthogonaux Inversion du cercle
Voir	Énigme des cercles qui tournent l'un sur l'autre Cercle – Index Géométrie – Index
Cette page	http://villemin.gerard.free.fr/GeomLAV/Cercle/Propriet.htm