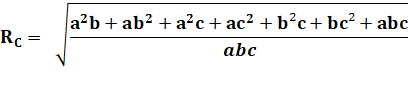|
|||||||||||||||||||||||||||||||||||||
![]()
|
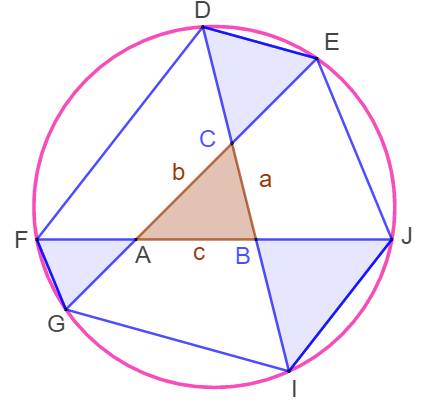
Cercle de Conway – Cercle des six points Cercle passant par six points situés sur les côtes prolongés d'un triangle quelconque. Imaginé par John Conway (1937-2020) |
|
|
||
|
Triangle quelconque ABC. Prolonger
les côtés et y déposer:
Les six
sommets des bases des triangles isocèles sont cocycliques. Ce cercle
est le cercle de Conway du triangle ABC. Les sommets forment un hexagone. |
|
|
|
|
|||
|
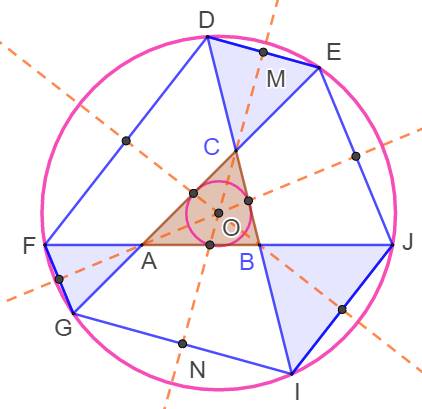
Avec médiatrices et bissectrices Médiatrice
MN du segment DE. Le cercle passant par D et E se trouve sur cette droite. Dans le triangle isocèle CDE, c'est aussi la bissectrice
de l'angle au sommet DCE C'est aussi la bissectrice de l'angle opposé par
le sommet ACB. C'est le cas pour les deux autres triangles
isocèles. L'intersection O des bissectrices est le centre du cercle inscrit
au triangle ABC. C'est par conséquent le point d'intersection des trois
médiatrices des bases des triangles isocèles. Donc les points D, E, F, G, I, et J sont sur le
même cercle de centre O et concentrique au cercle inscrit du triangle ABC. |
|
||
|
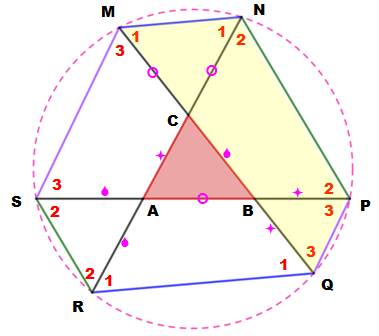
Avec les angles Les trois diagonales sont égales (isométriques) Les trois petits triangles sont isocèles, comme
le sont les triangles opposés (comme CMN et CRQ). Avec le même angle au sommet (C), les angles à la
base sont égaux (1). Idem pour les deux autres. Notez que, par conséquent, les côtés opposés de
l'hexagone sont parallèles. La somme
des angles dans un hexagone vaut 4 x 180°. Elle vaut aussi: 4 x (1 + 2 +
3). Prenons le quadrilatère jaune (MNPQ). La somme
des angles opposés (1 + 2 3) vaut
180°. Ce quadrilatère est inscriptible dans un cercle. Idem pour les deux
autres. L'hexagone de Conway est inscriptible dans un
cercle. |
|
||
|
|
||
|
Quelques
beautés ! |
|
|
|
Avec r le
rayon
du cercle inscrit et s le demi-périmètre du triangle, le rayon du cercle
de Conway se calcule avec: |
|
|
|
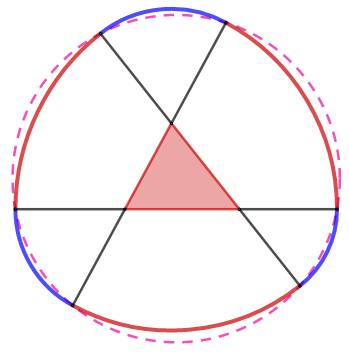
Cercle
de Reuleaux construits sur les points du cercle de Conway. Pour les six arcs de cercle, les centres sont les
sommets du triangle. |
|
|
|
|
||
|
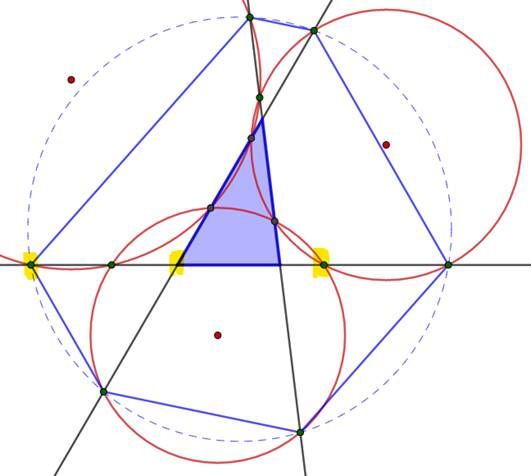
Un triangle bleu. Le cercle de Conway (pointillés bleus) avec ses
six points (en vert). Les centres des trois cercles
exinscrits du triangle. Trois cercles (en rouge) depuis ces centres et
passant par deux des points de Conway Les intersections définissent six points
supplémentaires (verts) qui se trouvent sur les droites portant les côtés du
triangle. Chaque point de Conway a une image symétrique par
rapport à un des sommets du triangle (exemple en jaune). |
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()