|
Édition du: 22/05/2022 |
|
INDEX |
CERCLE - PARTAGE |
||
|
Partage – Égalité |
|||
Faites un double-clic pour un retour en haut de page
![]()
|
PARTAGE du CERCLE* en parts égales avec des parallèles à un diamètre Partager
le cercle en parts égales (secteurs
de même aire) est un problème
connu. Ce n'est pas toujours possible de construire cette partition à
la règle et au compas.
Impossible
à la règle et au compas; et, même, le calcul des dimensions consiste à
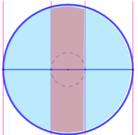
résoudre numériquement des équations transcendantales. Exemple de partition en trois. Pour un cercle de
rayon unité, la larguer de la bande centrale est proche de 0,53. L'aire de chaque
zone vaut Pi/3 soit environ 1,047. |
||
|
|
Sommaire de cette page >>> Partage du quart de cercle en deux >>> Partage du cercle complet en trois >>> Bilan |
Débutants Glossaire |
* Plus exactement du disque.
|
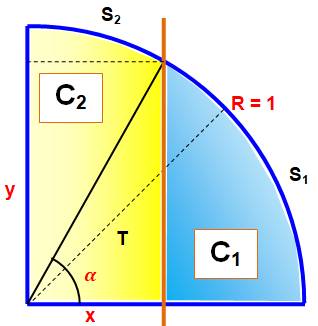
Objectif Dans ce quart de cercle, calculer la valeur de x
telle que la zone jaune ait la même aire que la zone bleue: C1
= C2 = Pi / 8 = 0,39269908… Approche Calcul de chaque aire à partir des secteurs S1
et S2 qui les interceptent avec ajout ou suppression du
triangle rectangle noté T. Les dimensions x et y de ce triangle sont le
cosinus et le sinus de l'angle alpha (avec le rayon unité). Il est alors possible de résumer l'égalité des
aires par une équation en alpha dont la résolution se fera par approche
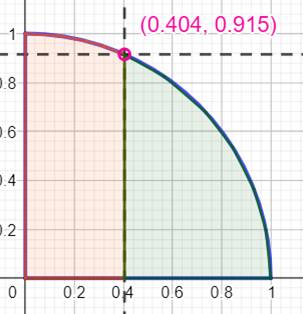
numérique (ou avec un logiciel de calcul). En l'occurrence, x = 0,4039
…, voisin de 2/5. |
|
|
|
Calculs
Graphique (deux solutions car x et
y peuvent être inversés, soit une rotation de 90°)
|
||
Pour ceux qui préféreraient le
calcul par intégration
Sachant que pour chaque x, la valeur
de y² est 1 – x²
L'inconnue est une borne d'intégration.

|
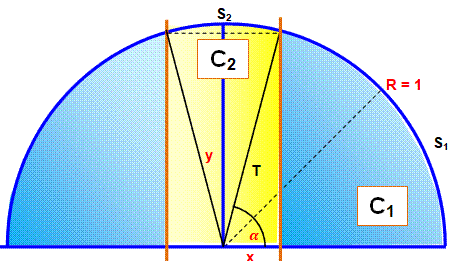
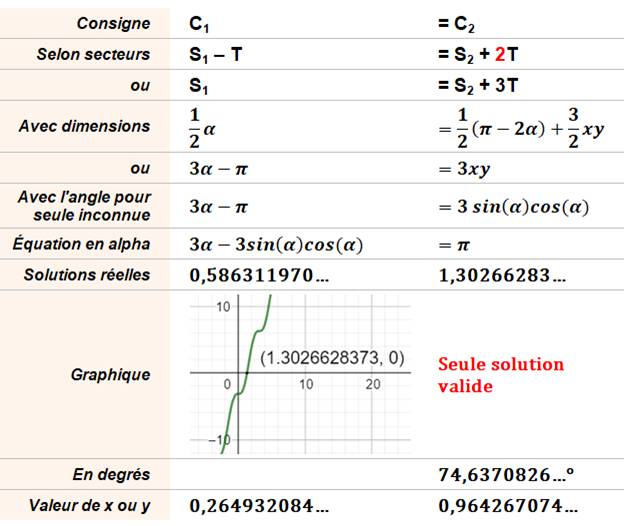
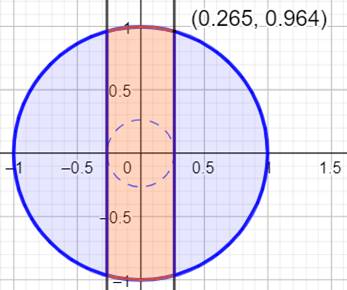
Objectif Dans ce demi-cercle (ou dans le cercle), calculer
la valeur de x telle que la zone jaune ait la même aire que chaque zone
bleue: C1
= C2 = Pi / 6 = 0,5235977… Approche Même chose que pour le quart de cercle En l'occurrence, x =
0,2649… …, voisin de 1/4. |
|
|
|
Calculs
La largeur de la bande est égale
à: 0,529864168… Partage approximativement de la
façon suivante: 1,25 / 0,5, / 1,25. Graphique (deux solutions car x et y
peuvent être inversés, soit une rotation de 90°)
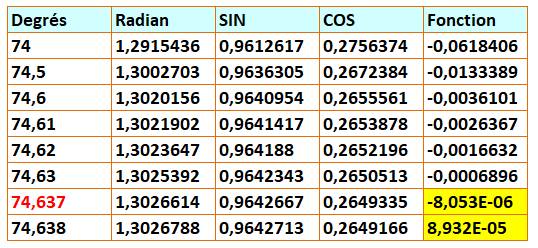
Résolution de l'équation en alpha
par tableur (passage de la fonction par zéro)
|
||
|
Il n'existe pas
de construction à la règle et au compas pour réaliser le partage du cercle
par des lignes parallèles à un diamètre. La solution
passe par la résolution d'une équation impliquant l'angle et ses lignes
trigonométriques. Il n'existe pas de solution analytique (en formule). La résolution
est possible:
Cette page
traite de la division par 2 et 3. Le même raisonnement peut être appliqué
pour d'autres partages. |
Page réalisée sur une
idée de Jean-Pierre
Sanguin
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |