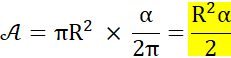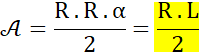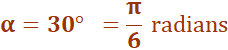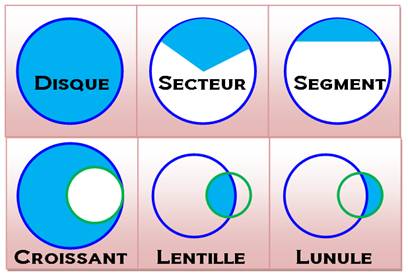
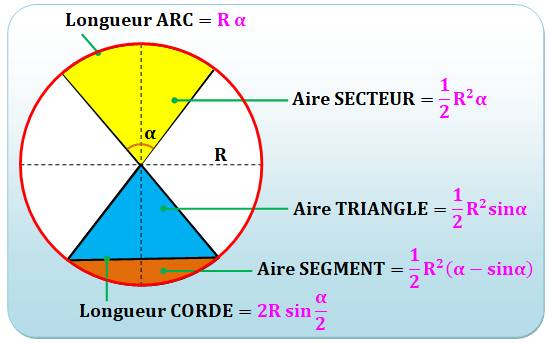
NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/04/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	CERCLE / DISQUE
Débutants Géométrie	Surface – Aire			Glossaire Géométrie
INDEX Aires Cercle Géométrie	Disque	Secteur	Segment	Lentille
	Disque et formes	Lunule	Croissant	Densité
	Couronne	Rosaces	Rectangle dans cercle
		Sommaire de cette page >>> Secteur de disque >>> Secteurs typiques >>> Anglais

Aires des éléments du cercle

SECTEUR

Voir en haut de page le lien vers l'un ou l'autre de ces éléments

Résumé

Secteur de disque
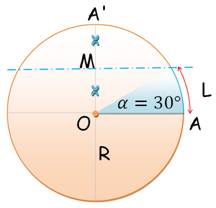
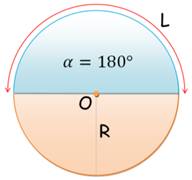
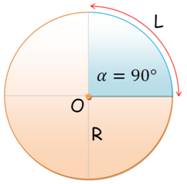
Secteur: portion du disque comprise entre deux rayons. La valeur de l'angle alpha suffit à définir un secteur. Pour être rigoureux, il faut aussi préciser l'angle béta que fait l'un des rayons avec un rayon de référence. Calculer la longueur de l'arc ou l'aire du secteur c'est prendre une fraction alpha du cercle complet. L'angle alpha est exprimé en radians, sachant que le cercle complet compte pour 2 Pi radians (360°). Si l'angle alpha est exprimé en degrés, remplacer le 2Pi du dénominateur par 360. Le périmètre du secteur est égal à L plus deux fois le rayon.
Notez l'expression de l'aire en fonction de la longueur L de l'arc. Formule semblable à celle de l'aire du triangle.

Secteurs typiques
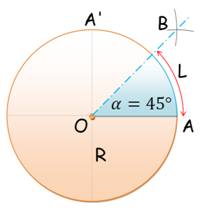
		On construit la bissectrice de l'angle droit AOA'.

On construit la médiatrice du segment OA'.

Propriété du cercle trigonométrique

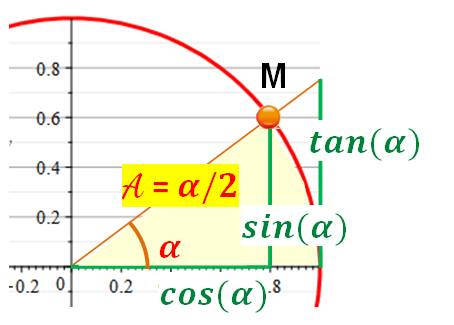
Voir Cercle trigonométrique / Analogie Cercle et Hyperbole

English corner
A circular sector or circle sector is the portion of a circle enclosed by two radii and an arc.

Retour	Cercle – Index
Suite	Segment de disque Angles Chèvre dans un enclos circulaire
Voir	Bissectrice Cône Géométrie – Vocabulaire Sphère Trigonométrie
Cette page	http://villemin.gerard.free.fr/GeomLAV/Cercle/aaaAIRE/Secteur.htm