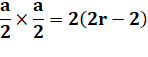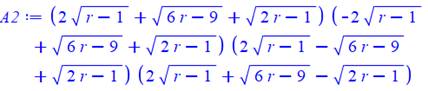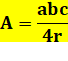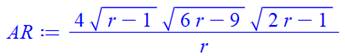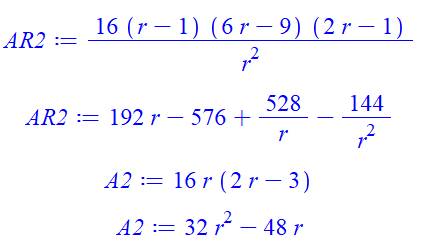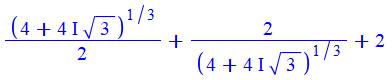Enigme du triangle inscrit dans le cercle

Édition du: 22/01/2024

INDEX Défis en géométrie Géométrie Jeux et énigmes	Énigmes en géométrie
	Quatre carrés	Tête géométrique	Carré et 2 Trg Équilatéraux
	Exercices 01	Escalier dans cercle	Rect et 2Trg Equilatéraux
	Triangles gigognes	Carrés dans cercle	Triangle dans le cercle
			Triangle dans carré

Faites un double-clic pour un retour en haut de page

TRIANGLE inscrit dans le CERCLE

Résoudre cette énigme qui semble abordable et pourtant, de nombreux amateurs s'y sont cassé les dents. Effectivement la solution passa par la résolution d'une équation du quatrième degré.

Sommaire de cette page

>>> Triangle inscrit dans un cercle

>>> Aire

>>> Rayon

>>> Solution

Débutants

Géométrie

Glossaire

Géométrie

Triangle inscrit dans un cercle		haut
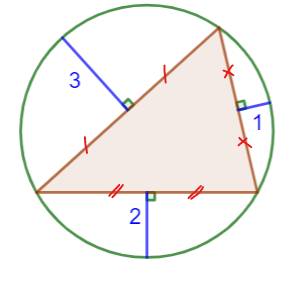
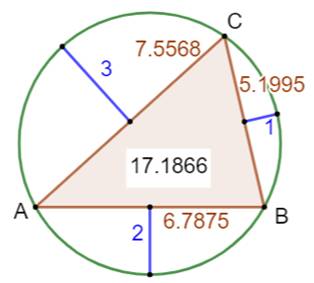
Problème La solution à ce problème n'est pas simple et la solution exposée ici doit beaucoup à Presh Talwalkar. On donne un cercle et un triangle inscrit. On connait la longueur des segments indiqués, portés par les médiatrices des côtés. Quelle est l'aire du triangle ? Longueur des côtés ? Indice Calculer les longueurs des côtés et l'aire en fonction du rayon du cercle, puis trouver la longueur de ce rayon.	Quelle est l'aire du triangle ? Pour info: cette figure est exacte en proportions.
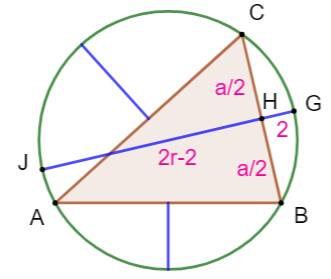
Solution : côtés en fonction de r Pour faire ce calcul, prenons le côté BC de longueur a et sa médiatrice qui porte la corde GJ de longueur 2r. Le théorème des cordes sécantes nous fournit cette équation: Même chose pour les deux autres côtés	Le centre du cercle circonscrit est le point de concours des médiatrices. La longueur de la corde portée par chaque médiatrice est égale au diamètre du cercle.

Voir Brève 50-987

Aire

haut

Calcul de l'aire

Avec la formule de Héron:

s étant le demi-périmètre.

Rayon		haut
Calcul du rayon Utilisation d'une autre formule pour l'aire en fonction de r le rayon du cercle circonscrit. Il faut résoudre en "r" l'égalité des deux expressions de l'aire: AR = A;
ou plutôt leur carré, et cela dans le but d'éliminer les radicaux. Mais attention aux solutions parasites induites.
Équation du quatrième degré pas simple à résoudre (ici, aide d'un logiciel mathématique).

Programme Maple

Solution n°2 avec radicaux

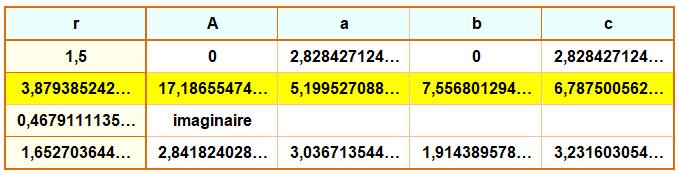
Commentaires

On pose les deux valeurs de l'aire au carré (A et A2).

Demande de résolution avec solve.

Évaluation séparée (evalf) de chacune des quatre solutions pour disposer d'une présentation lisible facilement.

On note que les parties imaginaires sont très petites et tendent vers 0 avec un calcul plus précis.

On donne l'expression avec radicaux de la deuxième solution (la seule valable).

Solution

haut

Les quatre racines de l'équation; mais, une seule solution valable.

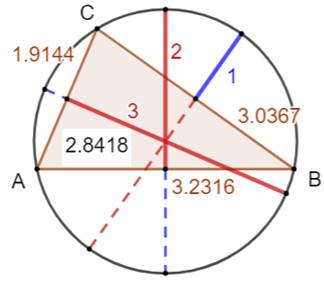
Validation de la solution: seule celle de la figure de gauche convient. Pour celle de droite, les longueurs sont respectées mais dans la configuration demandée.

Construction (Avec GeoGebra, par exemple).

Construire le triangle connaissant les trois côtés.

Construire le cercle circonscrit.

Construire les médiatrices des côtés du triangle.

Haut de page (ou double-clic)

Retour	Exercices sur le triangle – niveau lycée
Suite	Constructions élémentaires: triangle rectangle Résolution du triangle rectangle Doubler le triangle rectangle Quadrupler le triangle rectangle Triangles rectangles particuliers Types de triangles Triangle – Index
Voir	DicoMot Droite Égalités des triangles Enseignement – Collège Géométrie – Index Résolution du triangle quelconque Triangle de Pythagore
Sites	Impossible Viral Problem – Traingle in a circle – Presh Talwalkar Calcular el area de la region triangular ABC – old.reddit.com Inscribed Triangle in circle problem – Peeter Joot's Blog
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Exercice/TrianCer.htm