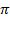NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 15/07/2019 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Constante
Débutants Constante PI	Généralités				Glossaire PI
INDEX Constante PI	Introduction	Calcul	Formules	Propriétés
	Historique	Valeur	Décimales	Curiosités
		Sommaire de cette page >>> Méthode des polygones >>> Algorithme d'Archimède >>> Algorithme d'Al Kashi >>> Formule de Viète

CALCUL de

La constante ne pourra jamais être connue avec plus de 10 ⁷⁷ décimales.

C'est le maximum calculable et mémorisable sur des supports physiques, selon certains.

En fin 2002, l'équipe de Kanada a calculé: 1 241 100 000 000 décimales.

Voir Actualités

MÉTHODE DES POLYGONES – Approche Calcul de l'aire à périmètre constant
Périmètre = 3 x 4 = 12 Hauteur du triangle: (4² – 2²) = 12 Aire = 212 = 43 = 6,92…	Périmètre = 4 x 3 = 12 Aire du carré = 3 x 3 = 9
Périmètre = 6 x 2 = 12 Hauteur triangle = (2² – 1²) = 3 Aire trg équilatéral = 3 x 1 = 3 Aire hexagone = 6 x 3 = 10,39…	Périmètre = 12 Rayon = 12/(2) = 1,91… Aire du disque = (1,91)² = 11,46…
À périmètre égal, c'est le disque qui occupe la plus grande surface.

Voir Principe du calcul en dodécaèdre / Isopérimètre

Algorithme d'Archimède

Méthode algorithmique de calcul d'aires et de volumes par exhaustion. Elle serait sans doute due à Eudoxe de Cnide (408-355 av. J.-C. ) Mais, c'est Archimède (287-212 av. J.-C.) qui la perfectionnée. Archimède Dans son texte " De la mesure du cercle", Archimède étudie successivement les polygones à 6, 12, 24, 48 et 96 côtés. Par encadrements successifs, il trouve que la valeur de Pi est comprise entre ces deux valeurs: dont la moyenne vaut: 3,1418… (trois décimales exactes). Il s'agit d'encadrer l'aire du disque par les polygones inscrits et circonscrits pour un nombre de côtés croissant. 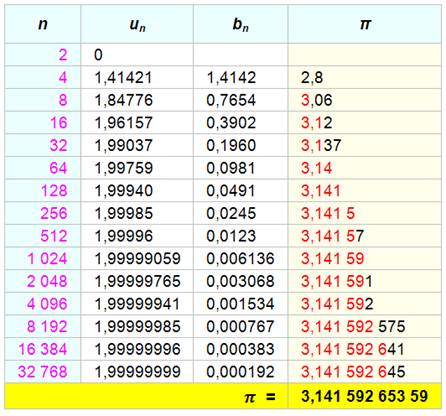Formules Avec un cercle de référence de diamètre 1, pn et Pn encadrent la valeur de . Calculs

Voir Méthode des bandes verticales et introduction au calcul intégral

Algorithme d'Al Kashi (environ 1436):
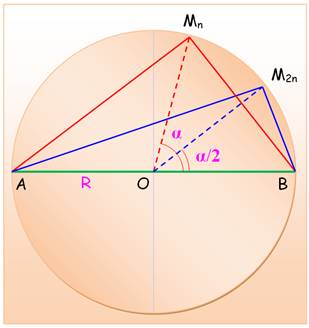
Notations bn = BMn b2n = BM2n un = AMn u2n = AM2n Formules bn^2 = 4R^2 – un^2 u2n^2 = R(2R + un)

Voir Algorithme / Al Kashi

Merci à Olivier Duwat pour sa lecture attentive

Formule de Viète (1540-1603)
En 1592, François Viète a trouvé une formule qui permet de trouver le périmètre du polygone lorsqu’on double le nombre de côtés. Son développement engendre la première formule infinie pour . Pour cela, il faut utiliser la formule:	Passage du carré à l'octogone inscrits dans le cercle. Les angles successifs sont /2 pour le carré, /4 pour l'octogone, /8 pour le polygone à 16 côtés …

Voir Produit de Wallis / Formules pour Pi

Algorithme de Cusa (1401-1464)
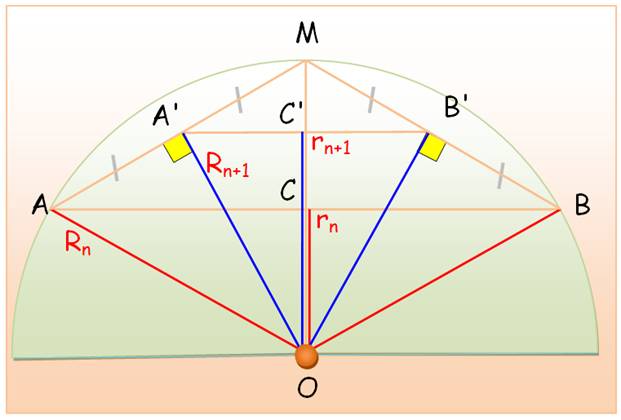
r2 = 1/2 rn+1 = (Rn + rn) / 2	R2 = 1 R3 = 1 / 2 = 2 / 4 Rn+1 = ( Rn . rn+1 )

Suite	Formules donnant Pi Pi - Glossaire Pi - Dictionnaire des nombres Cercle
Voir	Aire sous la parabole Arctg Calcul mental – Index Construction approchée de Pi Dodécagone Géométrie – Index Isopérimètre Nombres premiers dans Pi Racine de 8 Réduites de Pi - Calculs Théorie des nombres – Index
Site	L'Univers de Pi de Boris Gourevitch
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/PiCalcul.htm

Renvois de liens

>>> Réduites

>>>Séries égales à

>>>Formules avec arc tangente

>>>Les dernières formules de calcul de

>>>Méthode algorithmique de calcul de

>>>Chiffres de

>>>Gauss