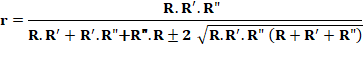|
|||||||||||||||||||||||||||||||||||||
![]()
|
Théorème de Descartes (1643 Théorème relatif à la
courbure de cercles tangents. |
Anglais: Descartes'
theorem
|
|
|||
|
Théorème Soit quatre cercles tangents entre eux. Si
k désigne la (inverse du rayon), alors: (k1 + k2 + k3+
k4)² = 2(k1² + k2² + k3² + k4²) |
|
||
|
Application:
courbure du quatrième cercle Avec C = 1/R, C = 1/R' et C" = 1/ R" = courbures des cercles initiaux Et c = 1/r, la courbure des cercles ajoutés:
La courbure est positive pour ce qui a trait à
l'extérieur du cercle et négative pour l'intérieur. Avec les rayons la formule devient:
Exemple avec R = - 1 et R' = R" = 1/2.
|
Sur cette figure si R = 1 alors r
= 1/3. Voir Construction de 1/3 |
||
|
Soddy Les deux cercles sont les cercles de Soddy et leur
centre les points de Soddy. Frederick Soddy (1877-1956) |
Epstein Les droites passant par deux points de tangences se
coupent en un point unique, le point d'Epstein. En fait deux point avec le cercle interne et le cercle externe. Valable aussi dans le cas de sphères. |
||
|
Avec
une droite Si un des cercles est une droite, sa courbure est
nulle.
Exemple
(Figure)
|
|
||
Voir Construction des deux cercles tangents à trois
cercles tangents
Anglais
|
In geometry, Descartes' theorem states that for every four kissing, or
mutually tangent, circles, the radii of the circles satisfy a certain
quadratic equation. By solving this equation, one can construct a fourth circle tangent to
three given, mutually tangent circles. The theorem is named after René Descartes, who stated it in 1643. |
Voir
Anglais pour le bac et pour les affaires
![]()
|
Suite |
|
|
Voir |
|
|
|
|
|
Cette page |
![]()