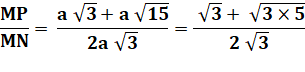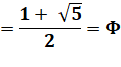NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 14/11/2024 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	Nombres d'or
Débutants NOMBRE D'OR	GÉOMÉTRIE				Glossaire NOMBRE D'OR
INDEX Suite de Fibonacci et nombre d'or Géométrie	Index	Introduction	Proportion	Construction
	Géométrie	Étoile	Aire Phi	Cercle
				Carré + Cercles
		Sommaire de cette page >>> Cercle >>> Ellipse d'or >>> Croissant de lune >>> De l'or dans les cercles

Cercle, croissant et ellipse dorés

Construction du nombre d'or au compas seulement

CERCLE et nombre d'or

Quel est l'angle qui partage un cercle en section dorée ?

Calcul:

Aire du disque: A = R²

Aire du secteur: A.y / 360

Aire du secteur complémentaire:
A (360 – y) / 360

Ratio des aires

A (360 – y ) / 360	=	360 – y
A.y / 360		y

Égalons ce ratio au nombre d'or:

360 – y = 1,618 y

2,618 y = 360

y = 137, 5077°

Remarquez que le ratio est indépendant de la notion de surface:

Il est aussi valable pour le périmètre.

Les aires des secteurs comme les longueurs des arcs
sont dans le rapport d'or.

ELLIPSE dorée
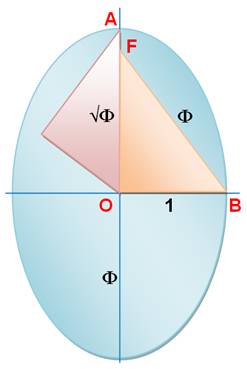
Elle est construite à partir du triangle doré de Pythagore: Le petit demi axe est OB = 1 Le foyer est en F avec OF = Φ Le triangle doré est basculé pour trouver le grand demi-axe OA = hypoténuse = Φ Il s'agit bien d'une ellipse de foyer F OF² = OA² - OB² (Φ)² = Φ ² - 1² Φ = Φ ² - 1² Voir Triangle d'or	Proportions respectées

Voir Ellipse dorée et cercles concentriques

CROISSANT de lune - Lunule
Deux cercles de centre A et B ayant un point commun O. Si OCO' est une section dorée, c'est le cas pour les segments tels que OPQ. Et, le point C n'est pas très loin du centre de gravité du croissant de lune. (Mais ce n'est pas le centre de gravité, comme l'affirme certains ouvrages!)

Voir Croissant et calcul du centre de gravité

De l'or dans les cercles
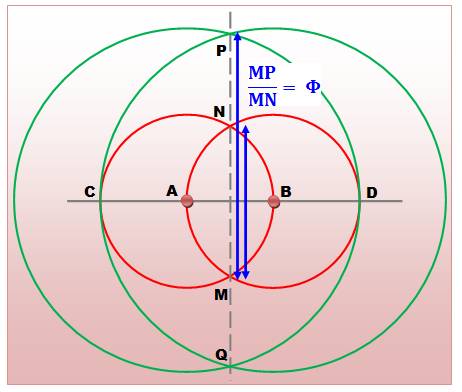
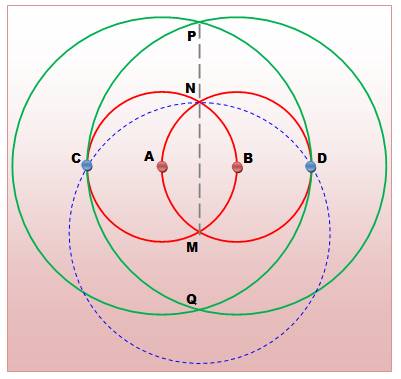
Propriété Le segment AB. Les deux cercles rouges A(B) et B(A). La droite AB les coupe en C et D. Les deux cercles verts A(D) et B(C). Par symétrie, les intersections des cercles M, N et P, Q sont colinéaires. Alors: MP / MN = nombre d'or Et aussi: MN / NP = nombre d'or Démonstration On note AB = 2a (convention).
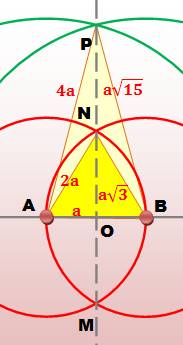
Dans le triangle AON	AO = a AN = 2a (rayon du cercle) ON = OM = a (Pythagore)
Dans le triangle AOP	AP = 4a (cercle de rayon double) OP = a (Pythagore)
Rapport

Construction au compas MN = 2a CM² = (a )² + (3a)² = 12a² = 3 x 4a² CM = 2a Le cercle de M(N) de centre M et passant par N, passe aussi par C et D. Pour construire la figure: Marquez les deux points A et B; Construisez les cercles rouges: Cercle M(N) qui définit les points C et D Construisez les cercles verts.

Construction due à K. Hofstetter: A simple construction of the Golden Section (2002)

Voir les références indiquées (en anglais)

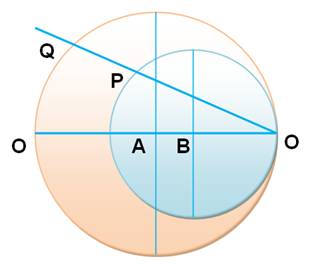
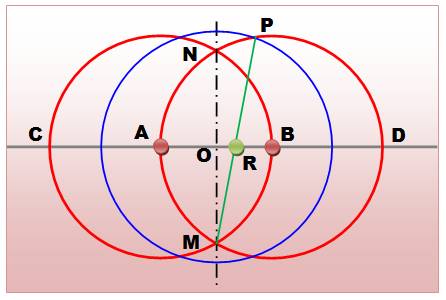
Division de AB en section dorée En 2005, Hofstetter récidive en trouvant cette construction qui divise le segment AB en section dorée: AR / RB = nombre d'or. Construction des cercles rouges comme précédemment. Cercle de centre M, avec AB pour rayon; il définit le point P. La droite MP coupe AB en G, le point de section dorée.

Suite	Géométrie et nombre d'or Valeurs du nombre d'or Construction Trigonométrie
Aussi	Cercle Constante Pi Constantes Mathématiques Construction géométrique des nombres Série du type Fibonacci et cousins
DicoNombre	Nombre 1,618…
Sites	Golden ratio in geometry – Cut the Knot Golden ratio by compass only – Cut the Knot Geometric construction of Phi in circles – The Golden Number
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/NbOrCerc.htm