NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 11/10/2018 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique Brèves de Maths
	CERCLE
Débutants Géométrie	Propriétés				Glossaire Géométrie
INDEX Cercle Géométrie	Cercle	Propriétés	Équations	Théorèmes
	Centre	Fondements	Angles	Partage
	Orthogonaux	Puissance	Inversion
		Sommaire de cette page >>> Intersection de deux cercles – Cercles orthogonaux >>> Cercle orthogonal passant par deux points du cercle >>> Cercle orthogonal passant par un point quelconque >>> Cercle orthogonal passant par deux points quelconques

CERCLES ORTHOGONAUX

Cercles tels que les tangentes aux deux intersections sont orthogonales (se coupent à angle droit).

Voir Trouver le centre et le rayon du cercle – Introduction

Intersection de deux cercles – Cercles orthogonaux
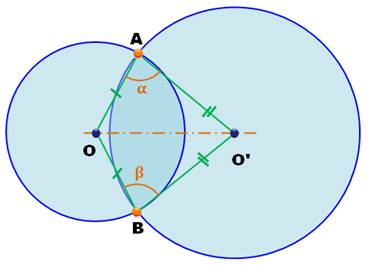
Démonstration Dans les triangles OAO' et OBO': OO' est un côté commun OA = OB = R O'A = O'B = R' Ces deux triangles sont égaux (isométriques). Leurs angles sont égaux deux à deux: l'angle alpha est égal à l'angle béta. Théorème Si deux cercles se coupent en A et B, les angles issus de A et B et interceptant les centres sont égaux. Cercles orthogonaux Deux cercles C et C' sont orthogonaux si l'angle alpha ou l'angle béta est égal à 90° (angle droit). On note:	Deux cercles quelconques Les angles alpha et béta sont égaux (même mesure). Avec 90°, les deux cercles sont orthogonaux.

Cercle orthogonal passant par deux points du cercle
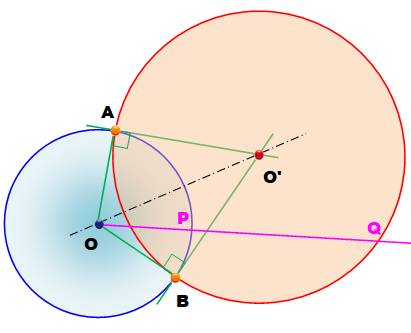
But Un cercle de centre 0. Tracez un cercle qui lui est orthogonal aux points A et B donnés. Construction Rayon OA et sa perpendiculaire en A. Rayon OB et sa perpendiculaire en B. Intersections de ces deux perpendiculaires en 0' Cercle de centre O' et de rayon O'A. Les droites AO' et BO' sont les tangentes au cercle O en A et B. Les droites AO et BO sont les tangentes au cercle O' en A et B. Ces quatre tangentes sont orthogonales deux à deux. Inverses Chacun des cercles est l'inversion de l'autre: OP. OQ = OA² = R²	Deux cercles orthogonaux Propriétés Lorsque deux cercles sont orthogonaux, les tangentes aux points d'intersection passent par le centre des cercles.

Voir Constructions élémentaires

Cercle orthogonal passant par un point quelconque
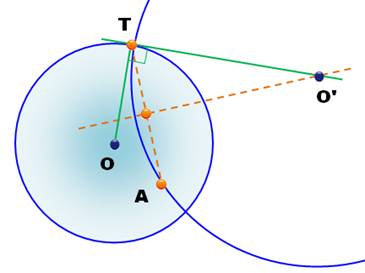
But Un cercle de centre 0. Tracez un cercle qui lui est orthogonal et passant par le point A. Construction Choisir un point T sur le cercle. Rayon OT et sa perpendiculaire p en T. Le centre du cercle cherché est sur la tangente p. Le centre du cercle passant par T et A est sur la médiatrice du segment AT. Ce centre O' est à l'intersection de la tangent et de ma médiatrice. Il en existe une infinité selon la position du point T.	Deux cercles orthogonaux dont l'un passe par A Le centre O' est l'intersection de la tangente en T et de la médiatrice de AT.

Cercle orthogonal passant par deux points quelconques
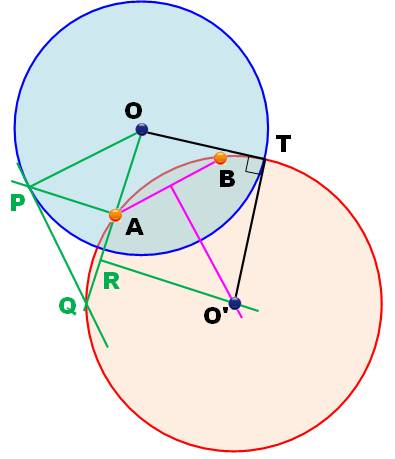
But Un cercle de centre 0. Tracez un cercle qui lui est orthogonal et passant par les points A et B. Construction Le point O' se trouvera sur la médiatrice de AB (rose) Pour construire le point Q sur OA (en vert): perpendiculaire en A à OA => P tangente en P => Q Médiatrice de AQ coupe la médiatrice de AB en 0', le centre du cercle orthogonal au premier cercle. L'angle OTO' est droit*: les deux cercles sont orthogonaux. * ce qu'il faudrait démontrer.

Suite	Arc de cercle – Coordonnées du point milieu Calcul de l'aire du cercle par intégrale Cercle d'Apollonius Théorèmes Cercle unité et triplets de Pythagore Programmation du dessin du cercle
Voir	Cercle – Index Géométrie – Index
Cette page	http://villemin.gerard.free.fr/GeomLAV/Cercle/Orthogon.htm