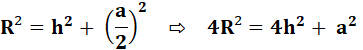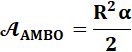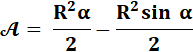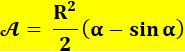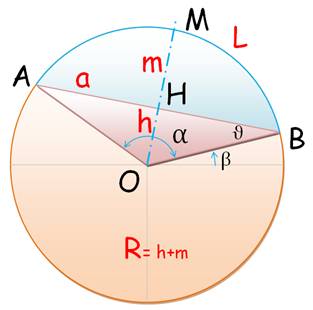
NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 19/06/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	CERCLE / DISQUE
Débutants Géométrie	Surface – Aire			Glossaire Géométrie
INDEX Aires Cercle Géométrie	Disque	Secteur	Segment	Densité
	Disque et formes	Lunule	Croissant	Lentille
		Rosaces	Rectangle dans cercle
		Sommaire de cette page >>> Segment de disque >>> Aire du segment >>> Aire inter-segments

SEGMENT DE DISQUE (segment circulaire)
Segment: secteur dont on a retiré le triangle isocèle (partie bleue de la figure). Segment: surface comprise entre l'arc AMB et la corde AB. La valeur de l'angle alpha suffit à définir un secteur. Pour être précis et positionner le segment sur le cercle, il faut préciser l'angle béta que fait l'un des rayons avec un rayon de référence.
Rayon du cercle connaissant le segment

Quelques repères sur cette figure
Arc AMB = L	L = R (angle alpha en radians)
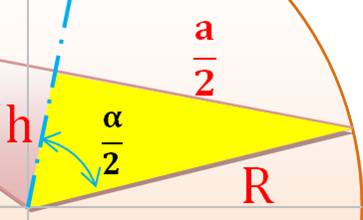
Figure (zoom)	Voir propriétés du triangle rectangle / Formules de trigonométrie
Pythagore
Angle
son double
Hauteur h
Corde a
Angle alpha

Notes: Arc cos s'écrit aussi cos^-1 (donne la valeur de l'angle lorsqu'on connaît son cosinus)
Voir Formules de trigo

Aire du segment
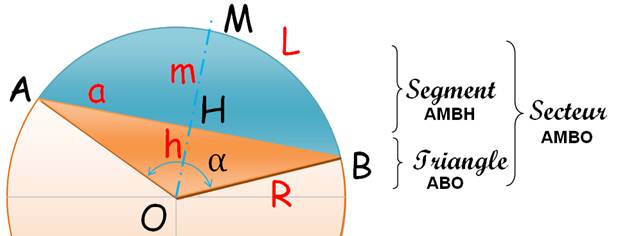
Segment	Aire segment = aire secteur – Aire triangle isocèle
Triangle isocèle ABO Voir Justification
Secteur AMBO Voir Justification
Segment AMBH
Expression avec L

Voir Application à l'énigme de la chèvre et de la grange

Expression de l'aire avec R et h

Secteur (à partir d'alpha sur deux)
Triangle
Segment

Cas typiques avec le cercle unité

Cas du cercle unité (R = 1)

Degrés	0	10	20	30	40	50	60
Radians	0	0,17453293	0,34906585	0,52359878	0,6981317	0,872664626	1,04719755
Sinus	0	0,17364818	0,34202014	0,5	0,64278761	0,766044443	0,8660254
Segment	0	0,00044237	0,00352285	0,01179939	0,02767205	0,053310091	0,09058607

Degrés	70	80	90	180	270	360
Radians	1,22173048	1,3962634	1,57079633	3,14159265	4,71238898	6,28318531
Sinus	0,93969262	0,98480775	1	0	-1	0
Segment	0,14101893	0,20572782	0,28539816	1,57079633	2,85619449	3,14159265

On vérifie que pour l'angle plein (360°), on retrouve l'aire classique du cercle; et la moitié pour 180°.

Aire inter-segments			haut
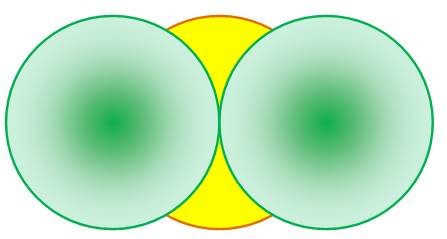
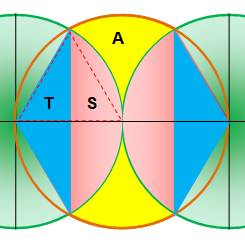
Question Quelle est l'aire de la zone jaune appartenant au cercle central occulté par ces deux cercles verts, tangents et de même rayon unité ?
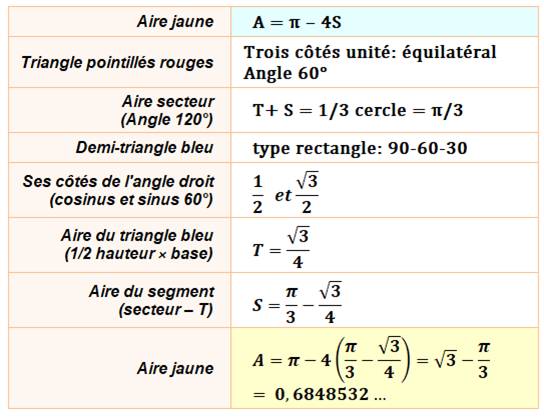
Solution L'aire cherchée correspond à celle du cercle rouge dont on retire quatre fois l'aire des segments S (rose). A = πR² – 4S Avec R = 1.
Calcul

Voir Brève 901

Retour	Secteur de disque Cercle – Index
Suite	Aire de l'intersection du rectangle avec le cercle Aire du carré Chèvre dans un enclos circulaire Lunule Angles Triangle de Reuleaux
Voir	Aire du segment de parabole Bissectrices Cône Géométrie – Vocabulaire Sphère Trigonométrie
Cette page	http://villemin.gerard.free.fr/GeomLAV/Cercle/aaaAIRE/Segment.htm