|
|||||||||||||||||||||||||||||||||
![]()
|
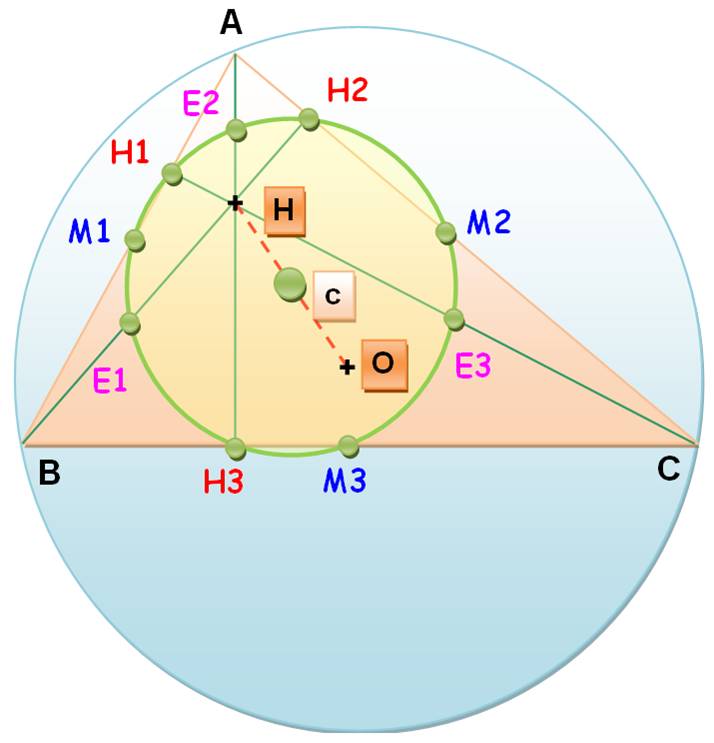
Cercle des neuf points Cercle d'Euler Cercle de Feuerbach On peut dire sans se tromper: cercle des neuf points. Par contre, ce cercle est plus connu sous le nom de cercle d'Euler, alors qu'il a été découvert et étudié par Feuerbach. |
|
|
|
|
|
|
|
|
|
|
alors, c le milieu de
OH, est le centre du cercle d'Euler. Depuis Euler et
Feuerbach
|
|
Voir Points remarquables du triangle / Brève 54-1060
|
|
|
|
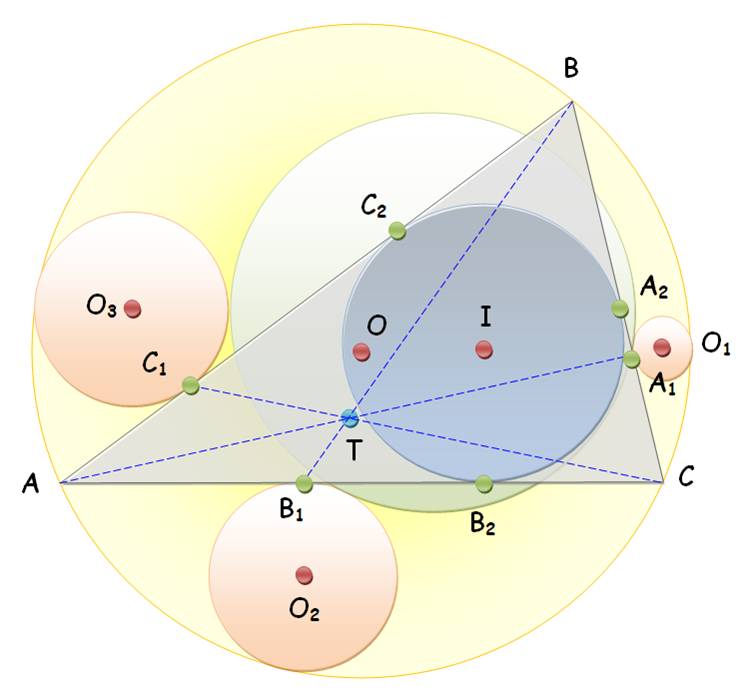
Généralisation Le théorème reste valable en remplaçant les cercles
exinscrits par des cercles, chacun tangent intérieurement au cercle
circonscrit et également au côté du triangle. Lev
Emelyanov - 2001
Théorème Les points de Feuerbach A1, B1 et C1 sont situés sur les côtés du
triangle ABC. On construit les trois cercles O1, O2 et O3 à
l'extérieur du triangle et tangents aux côtés du triangle en A1, B1 et C1 et,
aussi, tangents au cercle circonscrit du triangle ABC. Le cercle tangent extérieurement à ces trois cercles
est aussi tangent au cercle inscrit du triangle ABC si, et seulement si, les
droites AA1, BB1 et CC1 sont concourantes (en bleu pointillé sur la figure et
point d'intersection
en T). |
|
Voir Points remarquables du triangle
|
|
|
|
Euler, Leonhard
(1707-1783) – Mathématicien suisse >>> Feuerbach, Karl Wilhelm
(1800-1834) – Mathématicien allemand. 1822 - Il découvre le cercle des neufs points d'un
triangle. Ce cercle est parfois appelé, à tort, cercle d'Euler. Il prouve que ce cercle est tangent aux cercles inscrit
et exinscrits. Il a aussi introduit les coordonnées homogènes en 1827
en même temps que Möbius. Travaux également sur les points
cocycliques. |
|
Voir Contemporains en 1700 et en 1800
|
ENGLISH CORNER |
|
|
According to the
famous Feuerbach theorem there exists a
circle which is tangent internally to the incircle
and externally to each of the excircles of
a triangle. This is the nine-point circle
of the triangle. |
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()