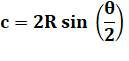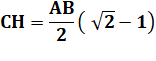|
|||||||||||||||||||||||||||||||||||||||
![]()
|
Construction du cercle sans le centre Comment construire un cercle ou un
arc de cercle sans accès au centre. Ce cas intervient dans le bâtiment ou les
jardins lorsque le centre est inaccessible (présence d'une fontaine, d'un
édicule, d'un mur …) Pas de solution simple ! Pour ces
cas pratiques, on se contentera souvent d'un tracé approximatif.
L'utilisation d'un gabarit est souvent le plus simple.
|
|
|
||
|
Pour
tracer un cercle
au sol en ayant accès au
centre, il suffit de planter un piquet au centre, de tendre une
ficelle de longueur égale au rayon souhaité. Avec un
plantoir, un clou ou une craie, marquer le sol en tournant autour du piquet,
ficelle bien tendue. |
|
|
|
Pour
tracer une ellipse
au sol en ayant accès aux deux foyers, planter deux piquets aux foyers et
tendre une corde fixée à ces deux piquets. Avec un
clou ou une craie, tendre la ficelle et marquer le sol en tournant autour des
piquets, ficelle bien tendue. Voir Ellipse
du jardinier |
|
|
Voir
Construction avec l'ellipse / Constructions
géométriques – Index
|
|
||
|
But Tracer un
arc de cercle de petite taille (quelques mètres max) sans accès au centre, devant un édifice,
par exemple. Principe L'idée est de construire la figure sur un terrain
libre et de relever la courbe sur un carton, une feuille de plastique ou encore des baguettes
assemblées à la façon d'un mètre pliant. Préparation Les deux points A, B sont les points par lesquels
doit passer le cercle. Reporter la longueur de la corde AB sur un terrain
libre. Partager la corde AB en deux parties égales et
tracer la perpendiculaire en H à AB. Positionner le point C selon la courbure
que vous désirez. Centre et rayon Pour trouver le centre et mesurer le rayon,
tracer un point D quelconque sur le cercle. La médiatrice de AD coupe la
droite CH au centre du cercle O. Tracé du cercle Mettre un piquet en O. Y attacher une ficelle. La
tendre jusqu'en C et y placer un clou ou une craie. Corde tendue, dessiner l'arc de cercle. Construire votre gabarit sur cette courbe. |
Arc de cercle en face d'un obstacle
Calculs Le rayon est donné par la formule indiquée. Par
exemple pour une corde de L = 10 m et une hauteur du segment de cercle de h =
2 m, le rayon du cercle vaut r = 7,25 m.
Voir Segment de cercle Idée de réalisation
|
|
|
|
|||
|
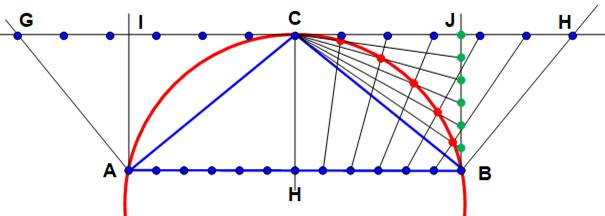
Principe Sur la corde, dessiner les perpendiculaires à
intervalles réguliers et mesurer la distance à l'intersection avec l'arc. Tracé de l'arc de cercle Reporter ces distances in situ. |
Illustration avec 5 valeurs
|
||
|
Calcul de x en fonction de d
Dans le triangle rectangle jaune (Pythagore):
qui conduit à l'équation du deuxième
degré: La résolution est fastidieuse sans outil
logiciel. Il est
plus pratique de dessiner le cercle et de mesurer ces longueurs. Exemple de calcul
ci-contre avec L = 10, h = 2 et donc R = 7,25
(cf. ci-dessus). |
Tableau avec 20 valeurs
|
||
|
|
||
|
But Tracer un
cercle en évitant un obstacle central. Principe Avancer d'une longueur et tourner d'un angle
donné. Recommencer jusqu'à fermer le polygone approximant le cercle. Voir Programmation
du cercle. Méthode Construire un gabarit représentant deux côtés et
le superposer de proche en proche Angle Choisir la quantité de côtés du polygone (ici : n
= 24). L'angle vaut 360 / n = 15° Coté Connaissant le rayon R du cercle à former, la
longueur du côté se calcule avec la formule:
Exemple pour R = 10 m
et angle de 15° (n = 24): c = 20 x sin (7,5°) = 20 x 0,1305 … = 2,610 … m |
Cercle approximé par un polygone 24
côtés
Gabarit de construction
|
|
|
|
|||
|
But Tracé un
arc de cercle en évitant un obstacle central. Méthode Choisir les trois points A, B et C. Construire le gabarit ACB avec deux liteaux, un
troisième en travers maintiendra l'ouverture de l'angle constante. Tous les points C tels que ce gabarit vise les
points A et B sont sur le cercle. En pratique Planter des piquets en A et B. Prolonger
suffisamment les segments CA et CB. Placer une pointe ou une craie en C. Faire pivoter le gabarit tout en le maintenant en
contact avec les piquets en A et B. Le point C décrit le cercle désiré. |
Principe L'angle qui intercepte la corde AB est invariant
quel que soit le point C sur le cercle (en restant du même côté). Voir
Angles
interceptant une corde Exemple d'arc de cercle à tracer
|
||
|
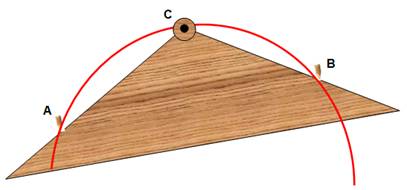
Outillages Un large triangle en bois passant par ABC Deux piquets en A et B; un clou en C (ou autre
instrument de marquage). Déplacer le triangle en se servant des deux
piquets comme guide. Le point C décrit un arc de cercle. Variante avec triangle plein |
|
||
|
|
||
|
But Tracé un
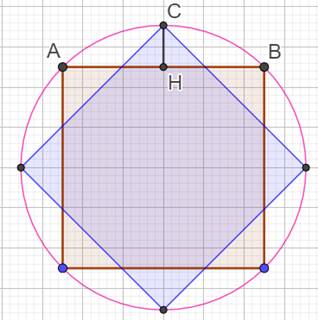
cercle en évitant un obstacle central. Approximation avec un octogone. Méthode Tracer un carré autour de l'obstacle central. Si
l'objet central est symétrique, prendre les mesures à partir de ses bords. Sur chacun des côtés, tracer la perpendiculaire
HC à AB, en son milieu. Marquer le point C à la distance calculée avec la
formule indiquée. Calcul et exemple avec AB = 10 m
Rayon du cercle
|
|
|
|
|
||
|
Tracer l'arc rouge sans accès au centre du cercle |
|
|
|
Méthode |
|
|
Merci à Patrice Bonsignour pour l'idée de cette page
![]()
|
Suite |
|
|
Voir |
|
|
Logiciel |
|
|
Site |
|
|
Cette page |
![]()