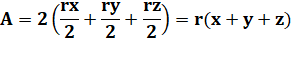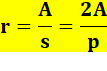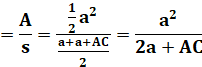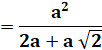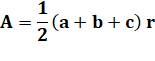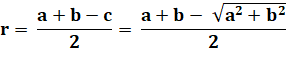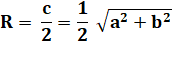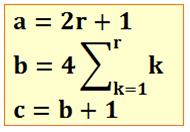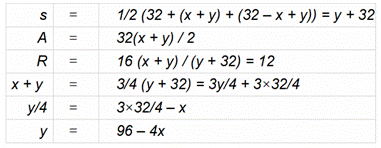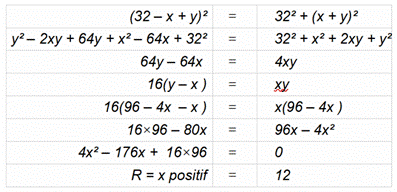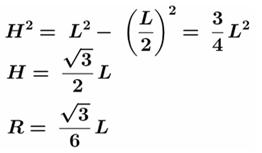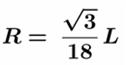|
||||||||||||||||||||||||||||||||||||||||||||||||||
![]()

Cercles dans un cercle –
Kandinsky
|
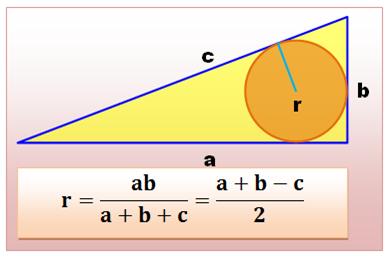
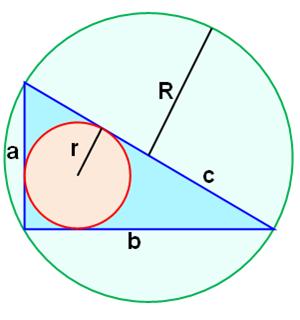
CERCLES INSCRITS Dans le triangle quelconque Calcul du rayon du cercle
inscrit. Dans le triangle rectangle de Pythagore (nombres
entiers) Le rayon du cercle inscrit
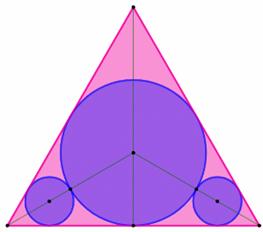
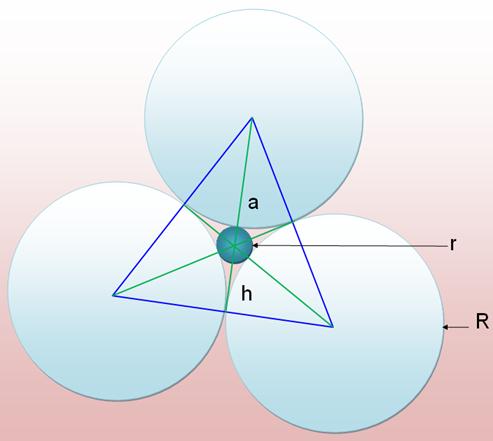
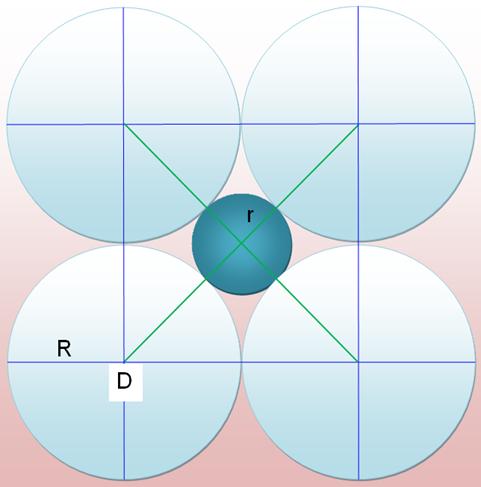
est aussi un nombre entier. Au milieu de cercles On dessine des cercles
identiques tangents entre eux. Une place se dégage au
centre. Quelle est la taille du
cercle inscriptible ? |
Voir Définitions
des trois types de cercles
|
|
||
|
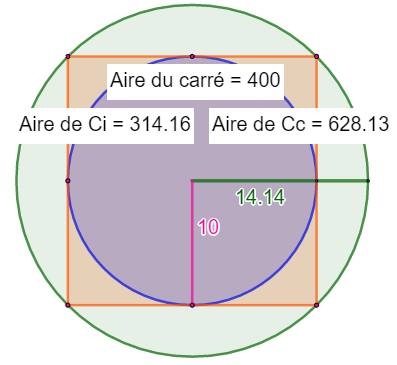
En bleu
le cercle inscrit dans le carré. Son diamètre est égal au côté du carré. Avec Pythagore,
on calcule la longueur de la diagonale du carré. On en déduit:
Sur la
figure RCC = 1,414 … RCI Le ratio
entre l'aire des deux cercles est donc égal à 2. L'aire de la couronne est
égale à celle du cercle inscrit. |
|
|
Voir Carré le plus grand dans k cercles
|
|
||
|
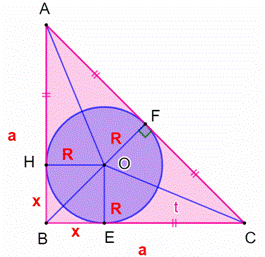
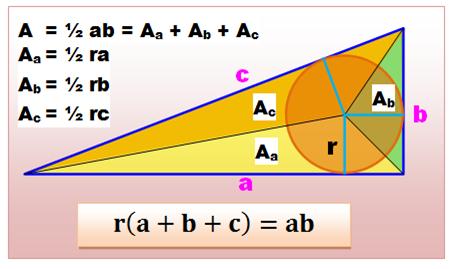
Le centre
du cercle inscrit O dans le triangle quelconque est le point de concours des
bissectrices (AO, BO et CO). Voir Les dix problèmes
d'Apollonius (LLL) Propriété des bissectrices: les
segments OPA, OPB et OPC sont égaux et perpendiculaires aux côtés. Ce
sont trois rayons du cercle inscrit. Les deux triangles de sommets A sont égaux (isométriques).
Même chose en B et C. L'aire du triangle est égale à la somme des aires
de ces six triangles.
En posant : a + b + c = 2 (x + y + z) = 2s
Le rayon du cercle inscrit est égal à deux fois l'aire divisée par le
périmètre du triangle. |
Les
triangles AOPB et AOPC sont égaux, car: -
Angles en A égaux; -
Angles droits en P; et - Côté commun AO. |
|
|
Et, en prenant la formule
de Héron pour l'aire:
|
|
|
Voir Coordonnées du centre
du cercle inscrit / Relations dans
le triangle quelconque / Problèmes d'Apollonius
Merci à Philippe
Morin pour sa relecture attentive
|
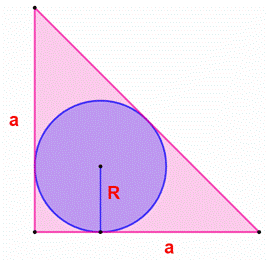
Résolution d’un théorème classique du triangle isocèle rectangle. |
||||||||||
|
Construction Un triangle
isocèle rectangle de côté a et son cercle inscrit de rayon R. Relation
entre R et a ? Piste Le rayon
du cercle inscrit dans un triangle est connu par la
formule : Calcul
|
Figure
Figure et ses propriétés
|
|||||||||
|
|
|||
|
Première relation (d'après
ci-dessus) A = ½ ab
et P = a + b + c r = ab /
(a+b+c) Deuxième relation Elle
résulte de la vérification suivante (utilisation du théorème
de Pythagore): (a + b + c) (a + b – c ) Cercle circonscrit Le
triangle rectangle est inscrit dans un demi-cercle et le rayon du cercle
circonscrit est c/2. |
Formules connues du Chinois Liu Hui (220-280),
prouvées par une dissection géométrique. Attention cette relation n'est valable ici que
parce que a² + b² = c² Aire du triangle = demi-périmètre x
rayon
|
||
|
Démonstration alternative En
comparant la somme du triangle complet à la somme des trois triangles le
composant. Les trois rayons dessinés vers les points de tangence étant les hauteurs
de ces triangles. |
|
||
|
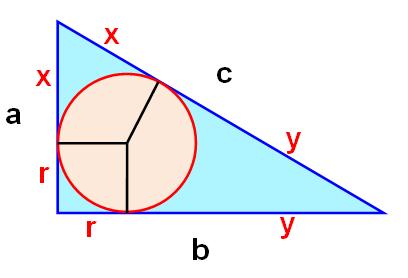
Autre démonstration (la plus
simple) Les segments tangents issus d'un même point étant
égaux: a = r + x b = r + y c = x + y a + b – c
= (r + x) + (r + y) – (x + y) a + b – c
= 2r |
|
||
|
Formules
|
|
||
Anglais: The inradius of a right triangle with integral sides
|
|
|||
|
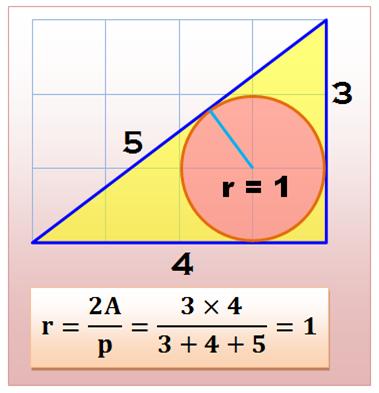
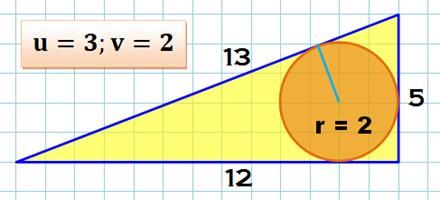
Approche Quel est
le rayon du cercle inscrit dans le fameux triangle
de Pythagore (3, 4, 5). En
appliquant la relation vue ci-dessus, il vient que r = 1, un nombre entier. Est-ce
toujours vrai ? Oui ! |
|
||
|
Généralisation Caractérisation
des côtés du triangle (triplet
de Pythagore). |
a = u² – v²,
b = 2uv, c = u² + v² Avec
u > v, tous deux des nombres entiers. |
||
|
Aire |
A = ½ (u² – v²) 2uv = uv (u – v) (u + v) |
||
|
Périmètre |
p = u² – v² + 2uv + u² + v² =
2u² + 2uv = 2u(u + v) |
||
|
Calcul du
rayon du cercle inscrit |
|
||
|
Théorème La longueur du rayon du cercle inscrit dans un triangle de Pythagore
est un nombre entier. |
|
||
Et les autres cercles?
|
Les longueurs ont également des nombres entiers
pour les rayons des trois cercles exinscrits Mais, ce n'est pas le cas du rayon du cercle
circonscrit qui vaut c/2, or dans un triplet primitif c est impair. |
|
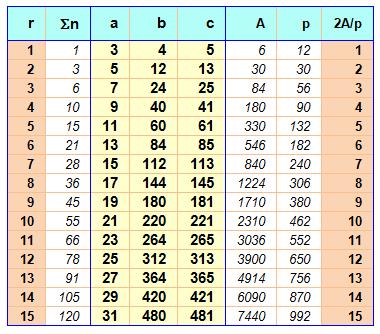
Exemple Avec u = 3 et v =2 a = 9 – 4 = 5 b = 2 x 3 x 2 = 12 c = 9 + 4 = 13 A = ½ 5 x 12 = 30 p = 12 + 13 + 5 = 30 r = 2A/p = 2 |
|
|
Relation entre (a, b, c) et r Cas de c = b + 1
Remarque Valable pour les triplets en (a, b, b+1) Ne donne pas, par exemple, les triplets:
|
Triplet (a, b, c) pour r de 1 à 15
|
Anglais: Circle inscribed in Pythagorean triangle
|
L’idée est de
recourir à la formule du rayon du cercle inscrit. |
||
|
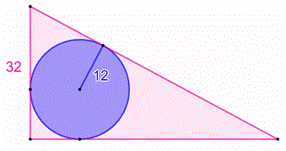
Construction
Un cercle de rayon
12 cm, inscrit dans un triangle rectangle dont le plus petit côté mesure 32
cm. Aire du triangle? Piste
On
connaît la relation entre aire (A), demi-périmètre (s) et rayon (R) du
cercle inscrit : R = A/s On sait aussi que
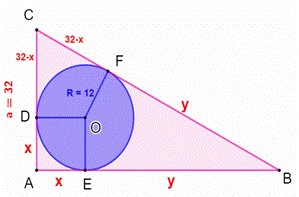
les segments de tangente
issues d’un même point sont de même longueur. Valeur
de y avec les tangentes
Valeur
de R = x avec Pythagore
|
Figure
initiale
Figure
et ses propriétés
Aire
du triangle x = 12 y = 96
– 4x = 48 A = 1/2
de 32 × (12 + 48) A = 960
cm² |
|
|
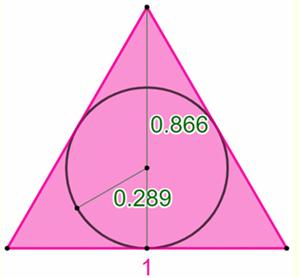
Cercle inscrit
dans le triangle équilatéral Avec le théorème
de Pythagore, on calcule :
R = 0,28867513459… L On se souvient que le centre
est au 1/3 de la médiane |
|
|
Cercle inscrit
dans le triangle équilatéral du sommet Même calcul que ci-dessus avec
une hauteur du petit triangle équilatéral égale au tiers de celle du plus
grand.
R = 0,0962250448651… L |
|
|
|
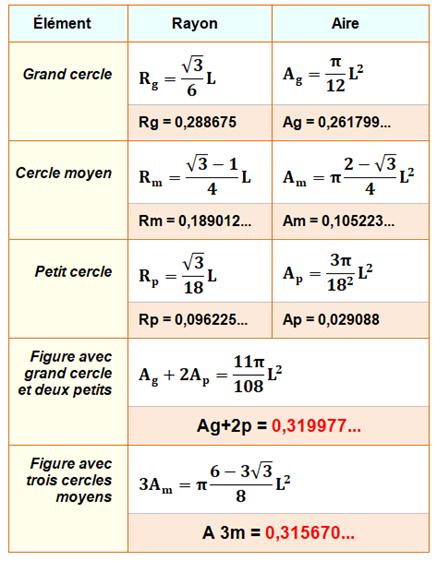
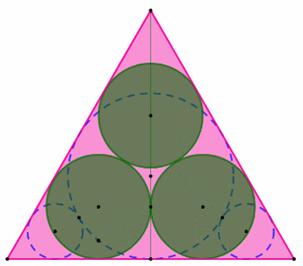
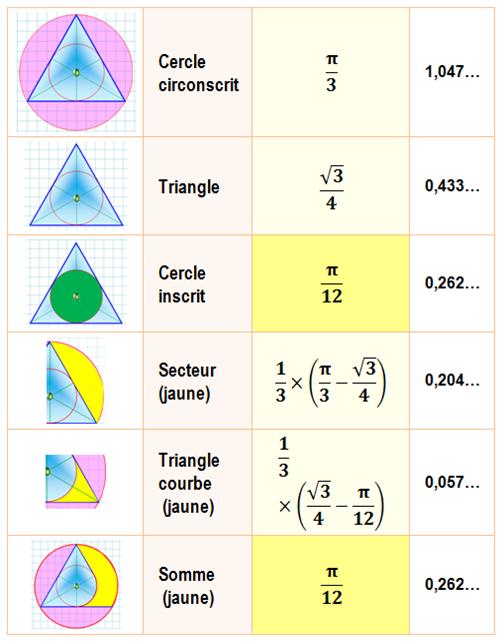
Comparaison entre aires des cercles inscrits Tableau des
calculs
Aire bleue – Aire verte =
0,00430… Soit 1,34…% de l'aire bleue. |
Triangle
avec grand et petits cercles inscrits
Triangle
avec cercles moyens inscrits
AIRE BLEUE > AIRE VERTE à proche de 1% près |
|
Voir Cercles inscrits dans le triangle
équilatéral
|
|
|
|
Avec le triangle équilatéral,
|
|
Voir Recherche du centre du cercle
inscrit dans le triangle équilatéral
![]()
|
|
||
|
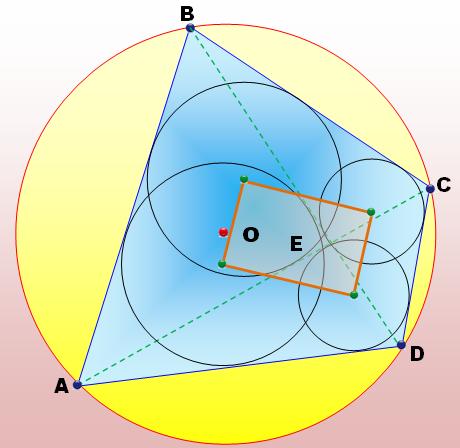
Théorème japonais pour les
quadrilatères inscriptibles ABCD un quadrilatère cyclique. Les deux
diagonales AC et BD. Les quatre
cercles inscrits dans les grands triangles formés avec les côtés et les
diagonales. Les
quatre centres de ces cercles sont les sommets d'un rectangle. |
|
|
![]()
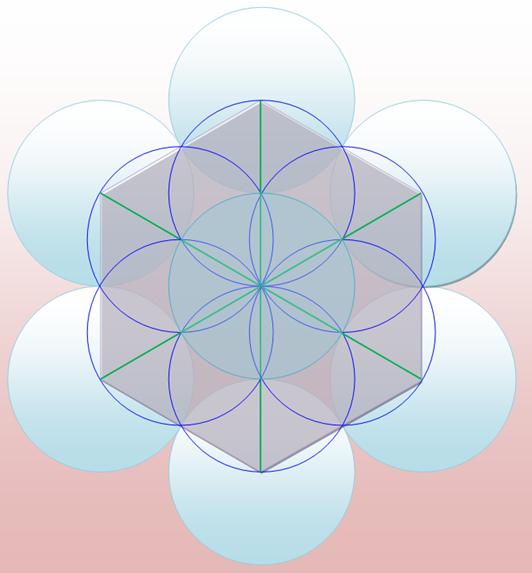
Cercles inscrits dans l'espace formé par n cercles tangents
|
|
|||||||||||||
Voir DicoNombre |
|||||||||||||
|
|
|||||||||||
|
3 cercles
Voir Orthocentre / Triangle équilatéral |
|||||||||||
|
4 cercles
Voir Carré |
|
5 cercles
Voir Pentagone |
|
Voir Hexagone / Construction / Rosace |
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()