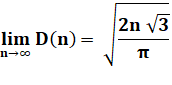|
Édition du: 10/02/2023 |
|
INDEX |
Cercle et points |
||
Faites un double-clic pour un retour en haut de page
![]()
|
Cercles et points Un ensemble de
points, distants entre eux de plus d'une unité. Quel est le rayon du cercle
minimal qui les englobe ? |
||
|
|
Sommaire de cette page >>> Cercle englobant n points à distance minimale >>> Quantité de cercles |
Débutants Glossaire |
|
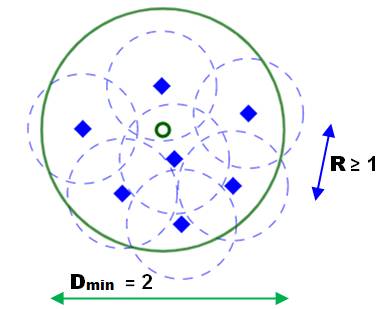
Exemple avec sept points Nous nous proposons de trouver le plus petit
diamètre D(n) d'un disque englobant un ensemble de n points tel que toutes
les distances mutuelles soient au moins égales à 1. L'illustration montre sept points. Le cercle de
rayon unité associé à chaque point définit la zone d'exclusion de tous les
autres points, sinon, ceux-ci seraient à une distance inférieure à une unité
les uns des autres. |
|
||
|
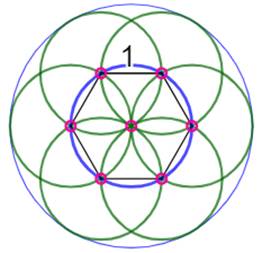
Théorème Un ensemble de
sept points mutuellement distance de 1 au moins est contenu dans un disque (y
compris la frontière) de rayon 1 au moins. Soit: D(7) = 2. Les sept points sont les sommets d'un hexagone
régulier accompagné du centre. Notez que le disque inclut sa circonférence. Bateman et Erdös ont prouvé ce théorème. |
Cas de sept points
|
||
|
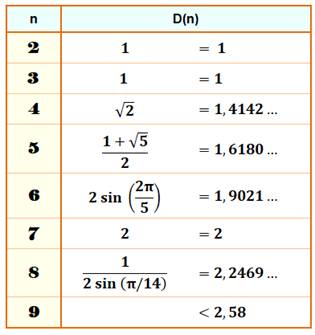
Construction Avec 2, 3, 4, 5, il s'agit des sommets des
polygones réguliers correspondants. Avec 6 et 7, il faut ajouter le point central aux
polygones
réguliers de côté 5 et 6. Valeurs de D(n)
|
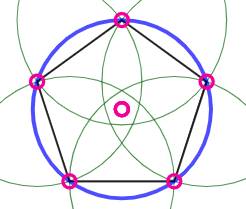
Cas de six points
Grand nombre Le comportement asymptotique de D(n) est connu
(Bateman et Erdös).
|
||
|
Théorème (1951 – Bateman
et Erdös) Il est impossible de disposer 20 points dans un
disque de rayon égal à 2, frontière comprise, alors que l'un est au centre et
tous les autres sont à une distance mutuelle d'au point 1. Pour reprendre le cas précédent, cela se traduit
par: D(20) > 2 |
Théorème Soit un ensemble de disques dans le plan, dont
aucun des centres n'est à l'intérieur d'un autre cercle. Soit le sous-ensemble de ces disques dont le
rayon n'excède pas celui de tout disque de l'ensemble de départ. Alors ce
sous-ensemble ne pas compter plus de 18 disques. |
|
Anglais
|
A set of seven points in the plane whose mutual
distances are all at least 1 has diameter at least 2, with this value
attained only by the set of points consisting of the vertices and circumcenter
of a regular hexagon of side length 1. |
Voir Anglais
pour le bac et pour les affaires
Haut de page (ou
double-clic)
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |