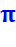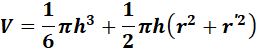NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 22/12/2021 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Géométrie
Débutants Géométrie	SPHÈRE				Glossaire Géométrie
INDEX Courbes Géométrie	Général	Aire et volume	Volumes proches	Sphère magique
	Empilements	Calotte …	Et cube	Sphère terrestre
		Sommaire de cette page >>> Index – Sphère >>> Approche >>> Propriétés >>> Sphère et cylindre >>> Équations >>> Paradoxe de Banach-Tarski		Devise: il faut sphère rire

SPHÈRE – Introduction et Index

Vocabulaire

La sphère est la surface qui délimite la boule.

Le cercle est la ligne qui délimite le disque.

Caractéristiques

Objet courbe qui n'est pas un polyèdre.

Objet parfaitement symétrique.

Tous les points de la surface sont équidistants du centre (rayon R).

Objet sans sommet et sans arêtes.

Objet formé d'une seule surface. Elle sépare l'intérieur de l'extérieur.

De tous les objets, la sphère est celui qui présente la plus petite aire pour un volume donné.

Formules

Aire du disque	Aire de la sphère	Volume de la boule
	A = 4 R^2 = D^2	V = 4/3 R^3
DISQ = R^2	A = 4 DISQ

Voir Rayon de la sphère inscrite ou circonscrite au cube ou à l'octaèdre / Valeur de Pi

Index SPHÈRE

Aire et volume - Méthode de calcul Ballon de football Calcul avec cylindre et cônes Calotte sphérique Conjecture de Poincaré Empilement des disques en 0,9069 Empilement des sphères Hypersphère Hypersphère et Poincaré Hypersphère et Univers Iso-Aire Paradoxe de Banach-Tarski Polyèdres proches de la sphère Segment sphérique Sphère de dimension 7 Sphère en n dimensions en 12 Sphère et cube Sphère inscrite et circonscrite dans le cube Sphère inscrite et circonscrite dans l'octaèdre Sphère magique Sphère terrestre Surface (aire) de la sphère en 12,56 Topologie et sphère Triangle sphérique Volume de la sphère - Méthode de calcul Volume de la sphère en 4,188 Volume de l'hypersphère en 5,25 Volumes comparés du cube et de la sphère Volumes proches DicoMot – Sphère Géométrie – Glossaire Géométrie – Index

Voir Expression avec le mot "sphère"

SPHÈRE – APPROCHE
Bulle ou surface de la sphère Ensemble des points situés à une distance fixe R d'un point donné. Boule ou volume de la sphère Solide engendré par la rotation d'un demi-cercle autour de son diamètre. Le point O est le centre de la sphère. La distance R = OA est le rayon. Le diamètre DD' est égal à deux fois le rayon. Deux points de la sphère D et D' opposés par le centre sont diamétralement opposés.

Anglais: Sphere, radius, diameter, antipode, bubble, ball

SEGMENT sphérique
Tranche d'une boule formée par la découpe de deux plans parallèles. Volume du segment sphérique

Voir Calcul du volume de la sphère par tranches

PROPRIÉTÉS de la sphère
Rayon Tous les rayons sont égaux à R. Tous les diamètres sont égaux à 2R	OA = OD = OP = … = R
Points Par deux points de la sphère diamétralement: opposés passent une infinité de grands cercles. Ces grands cercles ont tous la même longueur. non diamétralement opposés passe un seul grand cercle	APB, ADB, AD'B … PP'
La distance la plus courte sur la sphère entre deux points est une géodésique: arc de grand cercle entre ces deux points. Cette distance est appelée distance sphérique. Elle est mesurée par l'angle au centre qui intercepte l'arc. Cela est valable car tous les grands cercles sont de même longueur.	PP' POP'
Plan Toute intersection de la sphère et du plan produit un cercle ou un point si le plan est tangent à la sphère. Le cercle est minimum en ce point de tangence. Il est maximum lorsque le plan de section passe par le centre (et contient de ce fait un diamètre).	/
Propriété  Soit CC'P trois points de la sphère et du plan; Soit P un point de l'intersection du plan et de la sphère; La distance NP est fixe: P est situé sur un cercle de centre N de rayon r² = R² - h²	NP² = OP² - ON² = R² - h² = Constante
Le plan tangent est en contact avec un seul point T de la sphère. Le rayon OT est perpendiculaire au plan tangent.	/

Anglais: geodesic, great circle

SPHÈRE ET CYLINDRE

Considérons le cylindre circonscrit à la sphère: 

La surface du cylindre est égale à celle de la sphère.

Le volume entre le cylindre et la sphère vaut 1/2 sphère.

Voyons cela en formules:

ASphère	= 1	VSphère	= 2/3
Acylindre		Vcylindre

Pour le volume, on écrit aussi (ce qui revient au même).

VSphère	= 2
Vcylindre - VSphère

Archimède fier de ce résultat, le fit inscrire sur sa tombe.

Voir Démonstrations

Volume occupé dans le cube

La sphère occupe en gros la moitié du cube qui l'enveloppe.

Voir Comparaison des aires de la boule et du cube / Volume de l'hypersphère

ÉQUATIONS de la sphère

Cartésienne

x² + y² + z² = r²

Entre deux points

diamétralement opposés

(x-x₁) (x-x₂) + (y-y₁) (y-y₂) + (z-z₁) (z-z₂) = 0

Passant par 4 points

x² + y² + z² x1² + y1² + z1² x2² + y2² + z2² x3² + y3² + z3² x4² + y4² + z4²

x x1 x2 x3 x4

y y1 y2 y3 y4

z z1 z2 z3 z4

1 1 1 1 1

= 0

Polaire

x = r cosq sinj

y = r sinq sinj

z = r cosj

Paramétrique

u = r cosj

x =(r² - u²) cosq

y = (r² - u²) sinq

z = u

Généralisation

(ou la sphère est un cas particulier )

Ellipsoïde

x²	+	y²	+	z²	= 1
a²		b²		c²

Sphéroïde

x² + y²	+	z²	= 1
a²		c²

Hypersphère

x² + y² + z² + t² + … = r²

Paradoxe de Banach-Tarski
Paradoxe devenu théorème Il est possible de couper une boule en un nombre fini de morceaux et de réassembler ces morceaux pour former deux boules identiques à la première, à un déplacement près. Démontré en 1924 par Stefen Banach et Alfred Tarski.	Récréer deux sphères identiques à partir d'une seule est évidemment infaisable en pratique. Ce théorème fait appel à des notions situées aux confins des mathématiques avancées: Axiome de choix, Dénombrable et continu, Infini façon "hôtel de Hilbert" Théorie de la mesure

Voir Paradoxes / Brève n° 482 / Pour une explication claire voir la vidéo en référence

Sphère-robot (Rosphere)

Les chercheurs de l'Université de Madrid ont imaginé un robot sphérique, capable de se déplacer sur tout type de terrain. Il est mû par l'action d'un balancier interne qui déplace le centre de gravité, entraînant le mouvement de la sphère.

Actualité de juillet 2013

Suite	Aire et volume Voir Index
Voir	Cercle Deltaèdre Géométrie – Index Illusions d'optique Nombre d'argent Nombre d'or Nombres en cercle Polyèdres  Sphère terrestre Sphère magique Triangle sphérique Triangles Vocabulaire de la géométrie
DicoNombre	Nombre 0,52
Site	Théorème de Banach-Tarski – Deux minutes pour en parler – Vidéo
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/Sphere.htm