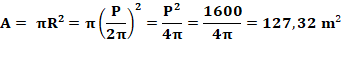|
|||||||||||||||||||||||||||||||||||
![]()
|
ISOPÉRIMÈTRE (Multiplicateur de Lagrange,
équation d'Euler-Lagrange) Quelle est la figure qui
offre la plus grande surface ? Le plus grand volume ? Le cercle offre 25% de
surface de plus que le carré à même périmètre. La princesse Didon de
Carthage connaissait déjà la réponse. J. Bernoulli a trouvé ce
résultat. |
|
Équation de la reine Didon |
|
|
|
La
corde
Approche |
||
|
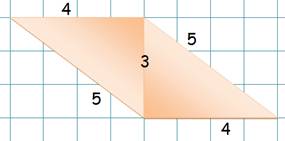
Losange:
|
|
|
|
Carré:
Son périmètre est plus petit, et
pourtant sa surface est plus grande. |
|
|
|
Rectangle:
|
|
|
|
Cercle:
Calcul
|
|
|
Voir Losange
/ Carré / Rectangle / Cercle
|
|
|
|
De tous les
rectangles et à même périmètre, c'est le carré
qui couvre la plus grande surface. Exemple: Le plus grand terrain rectangulaire
entouré avec une corde de 40 m, sera un carré de 40 /
4 = 10 m et son aire sera 100 m². Le côté du carré sera toujours le
périmètre divisé par 4. Il fera
mieux avec un cercle. Aire en fonction du périmètre:
|
|
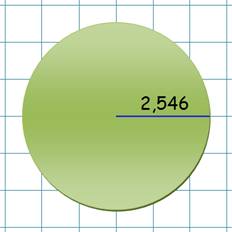
Voir Brève
546
|
|
|
|
Généralisation
Propriété Pour chaque type de
polygones et à même périmètre, c'est le polygone régulier qui couvre la plus grande
surface.
Question
suivante
|
|
|
|
|||
|
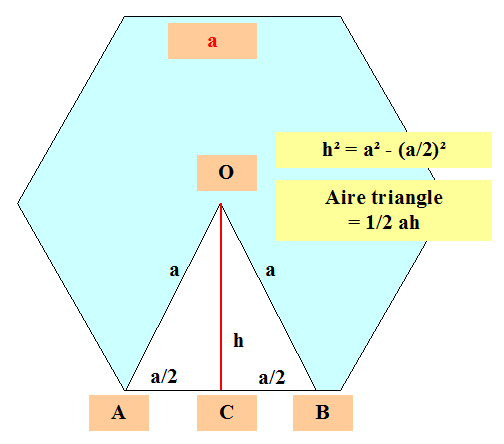
Figure
Propriété L'aire de l'hexagone est supérieure à celle du carré… Calculs |
|||
|
|
a h |
= 1 = ? |
|
|
|
OA
= AB = OB = a |
= 1 |
|
|
|
AC
= CB = a/2 |
= 1/2 |
|
|
h²
= a² – (a/2)² = 3/4 a² |
= 1 – 1/4 = 3/4 |
||
|
|
h
= a |
= |
|
|
|
A
= 1/2 ah = 1/2 a (a = a² |
= |
|
|
|
AH
= 6A = 6 a² = 3a² |
= 3 = 2,598… |
|
|
|
P
= 6a |
= 6 |
|
|
|
P
= 6a |
= 6 |
|
|
|
c
= 6a/4 = 3a/2 |
= 3/2 |
|
|
|
AC
= (3a/2)² = 9a² / 4 |
= 9/4 = 2,25 |
|
|
Généralisation |
|
||||||||||||
De tous les polygones réguliers et à
même périmètre, c'est celui qui a le plus de côtés qui couvre la plus grande
surface. Le cercle, "polygone
régulier" à nombre de côtés infini,
les surpasse tous. |
|||||||||||||
|
|
|
|
Cercles De toutes les figures et à même périmètre, c'est le cercle qui couvre
la plus grande surface. De toutes les figures de même aire, c'est le cercle qui a le plus petit
périmètre. Soit deux points et un arc de longueur donnée, c'est le demi-cercle
qui couvre la plus grande surface. Sphères De toutes les figures de même aire, c'est la sphère qui le plus grand volume. De toutes les
figures et à même volume, c'est la sphère qui a la plus petite aire. |
|
|
|
|
|
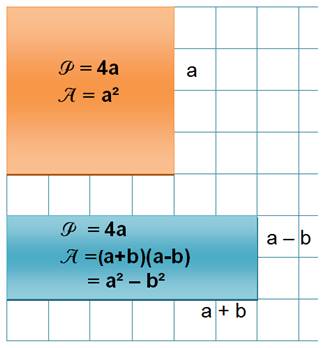
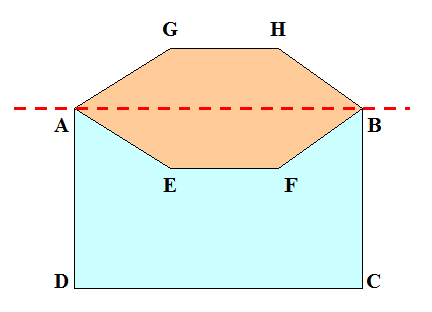
Convexe
PA EF BCD = PA GH BCD
Une forme concave peut toujours être remplacée par sa
symétrique convexe et obtenir une plus
grande aire à même périmètre. Demi-périmètre
et symétrie
La figure répondant
au problème présente une certaine symétrie: chaque fois que le périmètre est
coupé en deux parties de même longueur, l'aire maximum est obtenue lorsque
les surfaces de part et d'autre sont symétriques.
Demi-cercle
|
|
Voir Aire de la lunule
|
|
||
|
Anglais: Isoperimetric Inequality Des
théorèmes cités ci-dessus, on peut tirer les inégalités suivantes: |
S = Surface V = Volume |
|
|
Dans
le plan Égalité seulement pour le Cercle. |
|
|
|
Dans
l'espace Égalité seulement pour la Sphère. |
|
|
|
Cas
du rectangle Égalité seulement pour le Carré. |
Relation entre moyennes arithmétique
et géométrique |
|
|
|
|||
|
Antiquité
Didon Quelques siècles
avant J.-C. et selon la mythologie, la princesse Didon sœur de Pygmalion, roi
de Tyr s'installe sur la côte nord de l'Afrique avec quelques amis. Elle
forme de grandes surfaces semi-circulaires avec le diamètre longeant la côte.
C'est la ville de Carthage (ville tunisienne située au nord-est de la
capitale Tunis). Légende d’Elyssa-Didon.
Voir Volume maximum du cylindre pour aire
donnée Zénodore
Bernoulli
Steiner
Michael
Hutchings, Frank Morgan, Manuel Ritoré et Antonio Ros
|
|||
|
|
|
|
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()