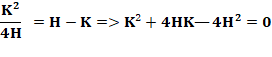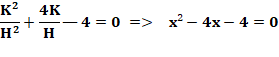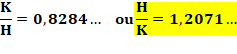|
||||||||||||||||||||||||||||||||||||||||
Voir Propriétés fondamentales
des triangles
![]()
|
Cercles et Rectangle Combien de cercles
peut-on ranger dans un rectangle ? Quel type de rangement ? Quel est le rayon des cercles inscriptibles dans
le rectangle
?
|
|
|
||
|
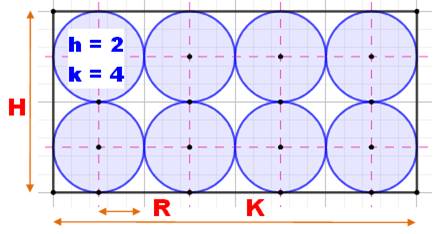
Empilement rectangulaire Taille de
la boite rectangulaire contenant q = h.k disques de rayon R.
|
Illustration
Application numérique h = 2 rangées; k = 4 colonnes; q = 8 disques R = 1 H = 2 x 2 x 1 = 4; K
= 2 x 4 x 1 = 8 ARect = 4 x 8 = 32 ADisk = 3,14 x 8 x 1² = 25,1327… Ratio: 78,53 % |
|
|
Empilement triangulaire (h est
impair) Empilement de h rangées de disques avec h = 2h' + 1 Dans ce
cas, les centres des cercles forment un treillis de triangles
équilatéraux. Hauteur
de chaque triangle: Taille de
la boite rectangulaire contenant q = h.k cercles de rayon R.
Note: les triangles
équilatéraux en pointillés indiquent comment construire cette figure. |
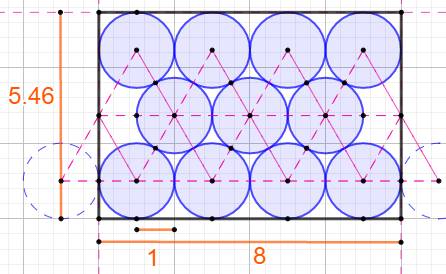
Illustration
Application numérique h
= 3; h' = 1; k = 4; q = 4 x 2 + 3 x 1 = 11 H
= (2 x 1,73 + 2) x 1 = 5,4641… K
= 2 x 4 x 1 = 8 ARect
= 8 x 5,46… = 43,7128… ADisk
= 3,14 x 11 x 1² = 34,5575… Ratio:
79,055 % |
|
|
Empilement triangulaire (h est
pair) Traitement
semblable. |
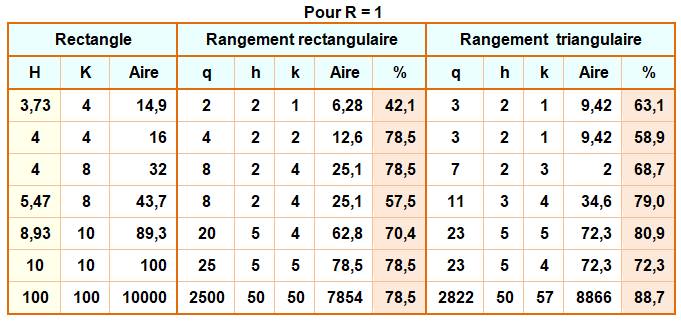
Pour
les applications numériques, voir le calculateur en ligne
indiqué. Le tableau suivant montre quelques ratios en comparant les deux
types de remplissage. |
|
|
Exemples avec Rectangle de
dimensions H et K données
Note: en rangement
triangulaire, la quantité de disques n'est pas égale à hk, car les rangées
intermédiaires comptent un disque en moins. |
||
|
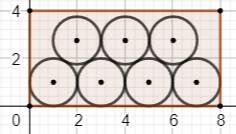
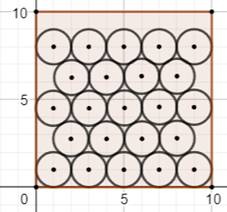
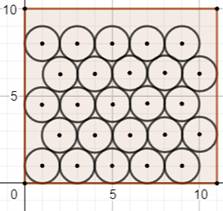
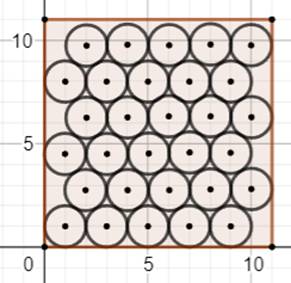
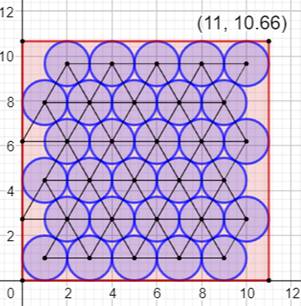
Illustrations de quelques cas (4; 8 =>
7), (10; 10 => 23), (10; 11 => 25), (11; 11 => 30) et (10,66; 11 => 30)
|
|
|
Programme Maple
|
But Pour H, K et R donnés, indiquer la quantité de
cercle en rangée (h), en colonne (k) et totale (Q). Commentaires Simple calcul des formules ci-dessus en tenant compte
des effets de seuil à l'aide de l'instruction floor
(plancher). Résultats Ce calcul illustre le cas limite illustré en
dernière image ci-dessus avec H en valeur limite pour six rangées: H = 2 + 5√3 = 10,6602540… |
Merci à Jérome Isoré pour l'idée de cette entrée
|
|
||
|
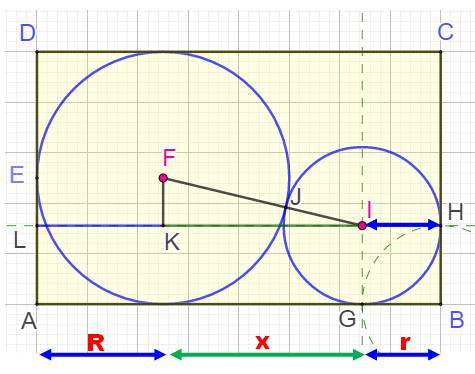
Défi On
dispose d'un rectangle de 16 x 10. Un cercle
de rayon 5 est inscrit, tangent à trois côtés. Quelle le
rayon du cercle le plus grand que l'on peut loger dans l'espace libre ? Observation Le second
cercle est tangent au grand et aux deux côtés du rectangle. |
|
|
|
Alignement L, K, I, H |
|
|
|
Application numérique |
|
|
|
Seule la plus petite racine est
conforme à l'épure |
|
|
|
Relation littérale et équation |
|
|
|
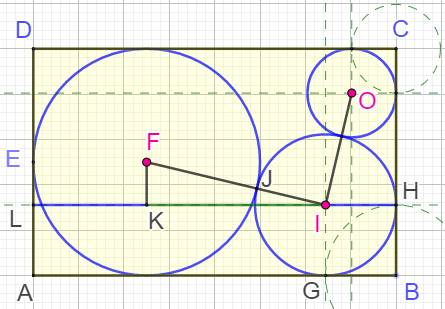
Un troisième cercle dans le
rectangle Ses dimensions: 10 x 6,2228… Calcul du rayon du nouveau cercle: 1,9553… |
|
|
|
|||
|
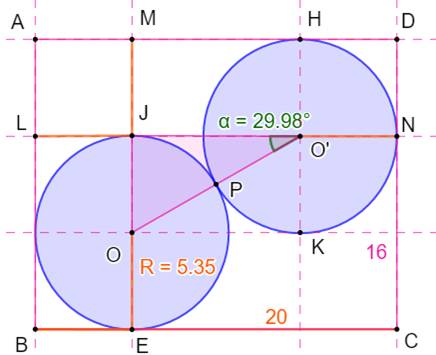
La boite
rectangulaire mesure 20 x 16. Quelle est le rayon des deux cercles identiques
les plus grands logeant dans cette boite ? La
géométrie est visible sur ce dessin. Nous allons calculer les dimensions du triangle
rectangle JOO': En
exprimant les dimensions du rectangle: |
|
||
|
En
isolant les lignes trigonométriques et en prenant les carrés. |
(2R sin |
||
|
En
sommant et en développant à gauche, sachant que sin² + cos² = 1 Soit, une
équation du second degré à résoudre. |
4R² = (H – 2R)² + (K – 2R)² 4R² – 4KR
+ H² + K² – 4HR = 0 |
||
|
Application
numérique avec H = 16 et K = 20. |
4R² –
144R – 656 = 0
R = 5,35089… et R = 30,649… |
||
|
|
||
|
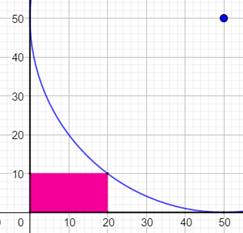
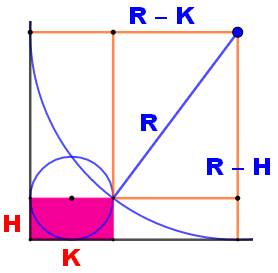
Défi On a un
rectangle rose: H = 10 e K = 20. Quel est
le rayon du cercle tangent aux côtés prolongés et passant par le sommet
opposé du rectangle ? Calcul R² = (R –
H)² + (R – K)² R² = R² –
2RH + H² + R² – 2RK + K² R² – 2(H
+ K) R + H² + K² = 0 Application numérique R² – 60R
+ 500 = 0 La
solution attendue pour R = 50. Mais une
seconde solution recevable avec R = 10, le petit cercle bleu. Solution
évidente qui permet de vérifier le calcul. |
|
|
|
|
||
|
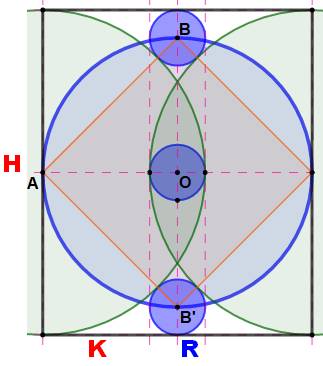
Sur cette
figure déterminer le rapport H/K. Dans le
triangle rectangle AOB: Théorème
de Pythagore: Sur le
segment central vertical, sachant que BB' est le diamètre du cercle bleu = K: En
remplaçant: Division
par H² et en posant x = K/H: Ce qui
donne: |
|
|
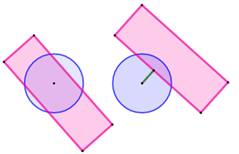
Intersection – Critère de détection
|
Un cercle coupe un rectangle si:
|
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Triangle/Propriet/CercRect.htm
|
![]()