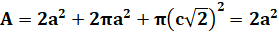|
||||||||||||||||||||||||||||||||
![]()
|
LUNULES ou croissants de Lune aussi:
lentilles ou ménisques La lunule est l'une des
surfaces qui apparait lorsque deux cercles
Note: La
lunule est la tache claire située sur la base de chaque ongle, sutout visible
sur le pouce. |
|
|
Voir Optique
|
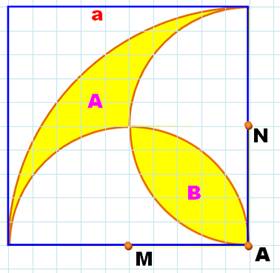
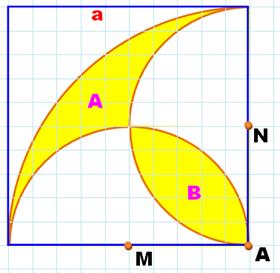
Un
carré (bleu) de côté a. Un
grand quart de cercle (A;
R = a) Deux
petits demi-cercles (M
et N; R = a/2) La
figure jaune qui ressemble à un poisson est partagée en deux parties dont
vous devez comparez les aires. Calculez également l'aire du poisson jaune. |
|
|
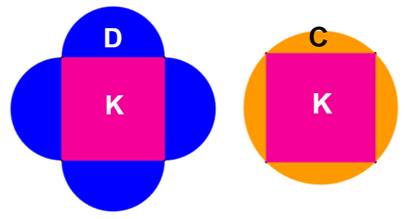
Construction Un
carré et son cercle circonscrit. Quatre
demi-cercles posés sur chacun des côtés du cercle. Quelle
est l'aire de la zone colorée en bleu ? Pistes Comment
décomposer la figure de façon à simplifier les calculs ? Solution Figure
en bas à gauche Prenons
le carré et les demi-cercles (K + D), lesquels couvrent toute la surface. Il
faut retirer les zones blanches. Figure
en bas à droite Prenons
le cercle et le carré. La zone à éliminer est ici en orange et sa surface
vaut (C – K). L'aire
de la zone bleue vaut: Si a
est le côté du carré:
|
Les
quatre lunules bleues ont
la même surface que le carré. |
|
Voir Brève 56-1111
|
Cette figure fait apparaître une
lunule dont l’aire vaut exactement 1 pour un disque de rayon 1 . |
||
|
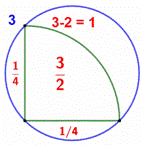
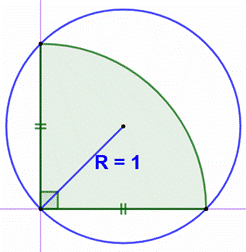
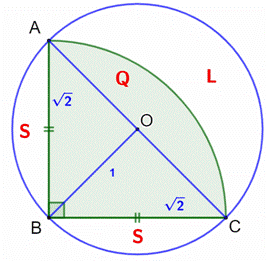
Construction
Un quart de
cercle dans un cercle. Quelle est
l’aire de la lunule bleue ? Pistes L’aire du
disque complet est égale à : Les triangles
OBA et OBC sont deux triangles isocèles rectangles identiques : Calculs
Aire du disque Aire du quart
de disque: Aire des
segments de cercle (quart de disque moins un triangle rectangle
isocèle): Aire de la
lunule : Note
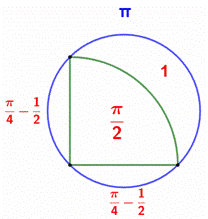
Aire du
segment Soit une approximation
des aires indiquée sur cette figure. Avec Pi pris égal à 3.
|
Figure initiale
Figure avec notations
Aires (exactes) avec
un disque de rayon unité
|
|
|
|
||
|
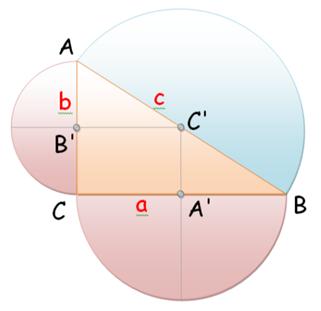
= = = Aire du demi-cercle en C' Notes: la figure
est plus jolie avec des demi-cercles, mais on aurait exactement la même
relation avec les cercles complets. En puriste, on aurait dû dire
aire des demi-disques
plutôt que demi-cercles. |
a² + b² = c² Cette propriété
montre que la somme des aires des demi-cercles mauves est égale à l'aire du demi-cercle bleu. |
|
|
|
||
|
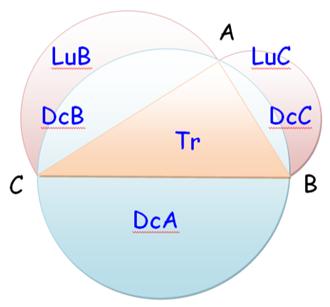
DcB + DcC = DcA DcB + DcC – DcA = 0
LuB + LuC = la figure au dessus de CB moins le demi grand
cercle, égal à DcA = DcB + DcC + Tr – DcA
LuB + LuC = Tr |
En
termes d'aires: Lunules =
petits demi-cercles + triangle auquel on retire le grand demi-cercle. Bilan: L'aire des deux lunules est égale à celle du triangle
rectangle. |
|
Voir Hippocrate et ses contemporains
Cas du
carré
|
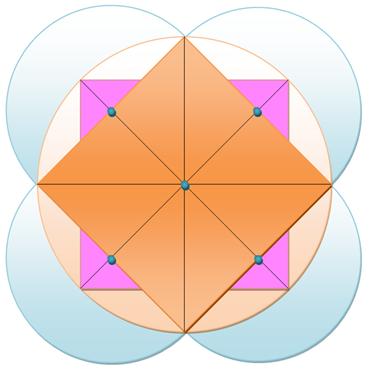
Sur
cette figure l'aire des quatre lunules (bleues) est égale à l'aire du carré
central (l'ocre ou le mauve). Cela
résulte de la propriété énoncée ci-dessus. Le triangle étant aussi isocèle et la figure est doublée
vers le bas par symétrie. L'égalité
entre aires originaires de cercles et de carrés avait laissé penser que la
solution de la quadrature du
cercle était là, sous-jacente. |
|
|
|
|
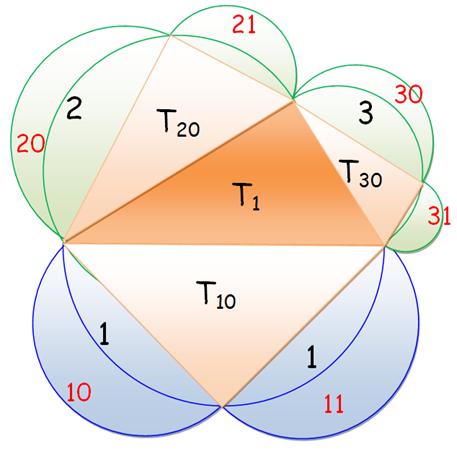
10 + 11 =
20 + 21+ 30 + 31 Aire bleue = aire verte
|
|
|
|
|||
|
|
|||
|
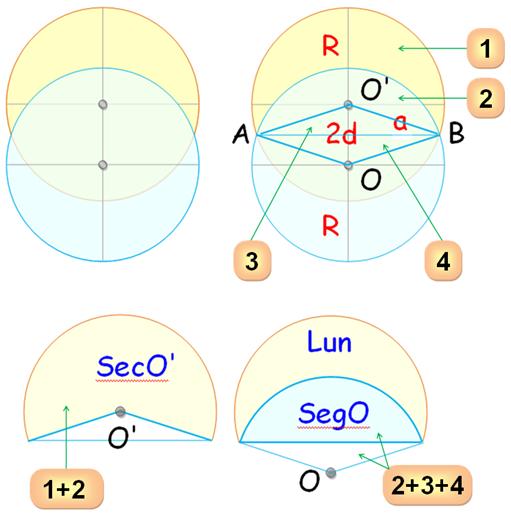
Secteur Segment Différence Lunule |
SecO' SegO SecO' – SegO 1 |
= 1 + 2 = 2 + 3 = 1 – 3 = SecO' – SegO +
3 |
|
|
Angles |
AOB AO'B
|
= = 2
|
|
|
Aire secteur Aire segment Aire du losange |
ASecO' ASegO ALos |
= ½ R² (2 = ½ R² ( = R² sin |
|
|
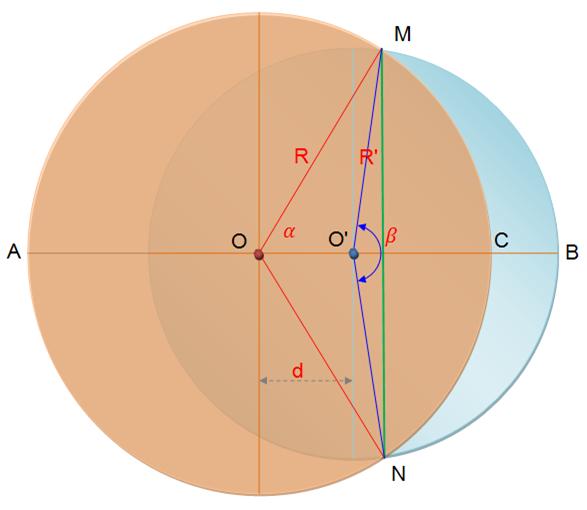
Aire de la lunule |
ALunule |
= ½ R² (2 – ½ R² ( + ½ R² sin = R² ( |
|
|
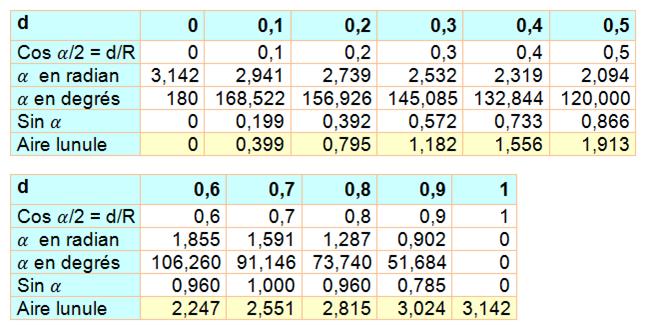
Quelques valeurs
|
|||
|
|
|||
|
|
|||
|
Lunule |
ALun |
= Aire MBN – Aire
MCN |
|
|
Aire MBN |
|
||
|
|
Aire MCN |
|
|
|
Bilan |
L'expression avec
R, R' et d n'est pas simple! Voir la page Lune de
Wolfram |
||
Voir Aire de la lentille
|
|
|
|
|
|
![]()
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
http://villemin.gerard.free.fr/GeomLAV/Cercle/aaaAIRE/Lunule.htm |
![]()