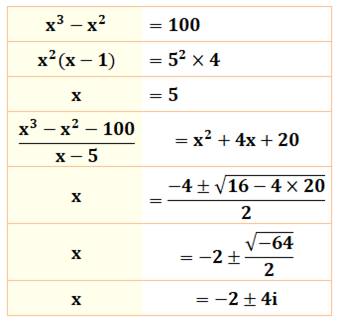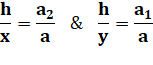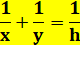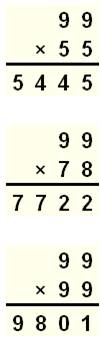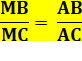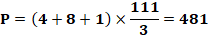NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 05/02/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Maths en se divertissant
Débutants Général	BRÈVES de MATHS									Glossaire Général
INDEX Brèves Atlas des maths	Page 1	Page 10		Page 20		Page 30		Page 40			Page 50
	Page 50 (980-999)		Page 51 (1000-1019)		Page 52 (1020-1039)		Page 53 (1040-1059)		Page 54 (1060-1079)
	Page 55 (1080-1099)		Page 56 (1100-1119)		Page 57 (1120-1139)		Page 58 (1140-1159)		Page 59 (1160-1179)

BRÈVES de MATHS – Page 55

Un millier de faits et chiffres

sur les nombres et les mathématiques

Ces pages sont dédiées à tous ceux qui veulent aborder les mathématiques en douceur et en s'amusant tout en découvrant les aspects les plus fondamentaux de cette discipline. Un parcours à picorer avec nombreux liens d'orientation vers les développements destinés à satisfaire votre curiosité.

En principe ces pages sont très abordables sans connaissances particulières de maths. Elles sont proposées dans un ordre quelconque favorisant la découverte de sujets multiples.

Anglais: Facts and figures about numbers and mathematics

1080. Calcul d'un produit
Produit de 2 à 5 nombres successifs: formule et exemple
Calcul avec cinq nombres successifs centrés sur 100 Le tableau montre le calcul pas à pas conformément à la formule indiquée ci-dessus. Ce calcul (98×99×100×101×102) est parfois présenté comme un problème de calcul à exécuter sans calculette.
Brèves associées	>>> Produit de deux nombres proches		>>> Brèves Calculs – Index
Pour en savoir plus	>>> Factorielle tronquée		>>> Défis viraux sur le net

1081. Résoudre x^3 –x^2 = 100
Problème et solution Le tableau montre l'équation du troisième degré à résoudre et ses trois racines dont deux sont complexes
Résolution Une factorisation à gauche comme à droite est possible. La valeur x = 5 semble convenir du fait de sa présence au carré. Cette valeur satisfait également le second facteur (5 – 1 = 4). La première racine est 5. Pour trouver la forme générique du second facteur divisons le polynôme du troisième degré par (x – 5). On obtient un polynôme du second degré dont on calcule les racines. Division
Brèves associées	>>> Racines par factorisation			>>> Brèves Équations – Index
Pour en savoir plus	>>> Équation du troisième degré >>> Équations			>>> Division des polynômes

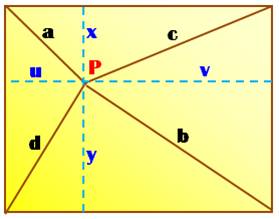
1082. Théorème du drapeau britannique British flag theorem
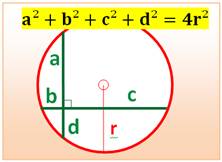
Construction et propriété Un rectangle et un point P quelconque interne ou externe, alors la relation suivante est vérifiée: a² + b² = c² + d² Démonstration avec le théorème de Pythagore a² + b² = u² + x² + v² + y² c² + d² = x² + v² + u² + y² Il y a bien égalité.
Brèves associées	>>> Théorème de Ptolémée		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Point et rectangle		>>> Quadrilatère

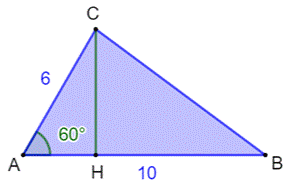
1083. Aire du triangle (a, 60°, b)
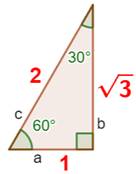
Construction Un triangle dont l'angle A est égal à 60%. La longueur des côtés adjacents est 6 et 10 cm. Calculer l'aire du triangle ABC. Piste L'aire du triangle est égale à: 1/2 AB × CH. Comment connaitre la hauteur CH ? À l'aide du triangle rectangle primitif (Figure du bas). En effet, tous les triangles rectangles (30, 60) sont semblables et ont donc les mêmes proportions. Solution Le triangle ACH a une hypoténuse AC = 6 qui est trois fois plus que celle du triangle primitif. La hauteur CH vaut donc: 3 × √3 Et l'aire devient: A = 1/2 × 10 × 3 × √3 = 15 √3.		Calculer l'aire de e triangle Triangle rectangle (30, 60) primitif
Brèves associées	>>> Triangle rectangle – Approche		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Aire du triangle (a, 60, b) – Détails		>>> Triangles semblables

1084. Aires de triangles dans un quadrilatère
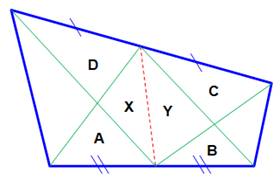
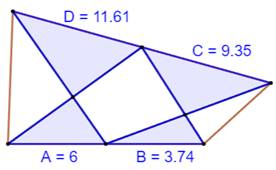
Construction Un quadrilatère et une médiane (pointillé rouge) Segments verts qui joignent les sommets du quadrilatère aux pieds de la médiane. Aires des triangles notées: A, B, C, D, X et Y. Quelle est l'aire de A connaissant B, C et D ? Piste La médiane d'un triangle le partage en deux triangles de même aire. D + X = Y + C A + X = Y + B Soustraction A = B – C + D ou A + C = B + D Exemple A = 3,74 – 9,35 + 11,61 = 6
Brèves associées	>>> Cinq quadrilatères	>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Aire du quadrilatère	>>> Quadrilatères

1085. Théorème de la double échelle
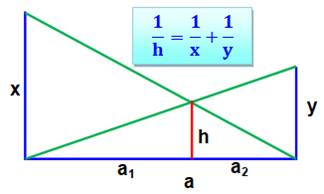
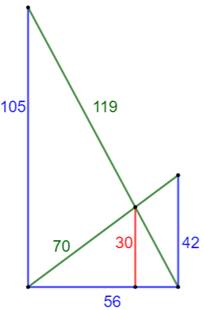
Échelle double (Cross ladder theorem) Deux parois verticales, ou non, de hauteur x et y. Deux segments verts. Hauteur h ? Propriété Théorème de Thalès Somme Division par h Exemple numérique La figure du bas montre la figure avec des longueurs toutes en nombres entiers. C'est un cas très rare.
Brèves associées	>>> Longueur de la rampe d'escalier		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Théorème de l'échelle double		>>> Cas du puits

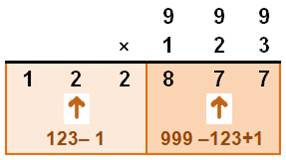
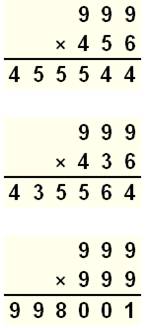
1086. Multiplications par 99 ou 999
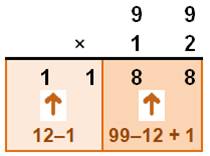
99 × 12 = 1188 Autres exemples		999 × 123 = 122977 Autres exemples
Brèves associées	>>> Multiplication par 9…9		>>> Brèves Calculs – Index
Pour en savoir plus	>>> Multiplications à deux chiffres		>>> Nombre 99 >>> Nombre 999

1087. Quadrilatère circonscriptible
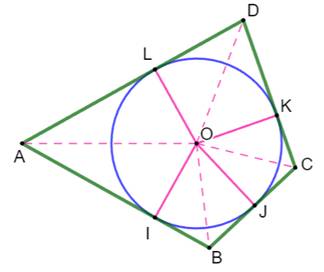
Définition Un quadrilatère circonscriptible ou tangentiel est tel que ses quatre côtés sont tangents à un même cercle. Propriété Tous les segments comme AL et AI, issus d'un point et se terminant au point de tangences, sont de même longueur. L'aire du quadrilatère est égale à celle du cercle multiplié par le demi-périmètre du quadrilatère. Démonstration Somme des aires des triangles qui composent le quadrilatère: A = ½ R٠AB + ½ R٠BC + ½ R٠CD + ½ R٠DA A = ½ R (AB+BC+CD+DA) = ½ R٠P Propriété des côtés Avec AI = AL, BI = BJ … on a: AI + BI + DK + CK = AL + BJ + DL + CJ En sommant: AB + CD = BC + DA		R: rayon du cercle inscrit P: périmètre du quadrilatère
Brèves associées	>>> Quadrilatère – Centre de gravité		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Quadrilatère >>> Quadrilatère inscrit – Aire		>>> Circonscriptible

1088. Trapèze – Propriétés
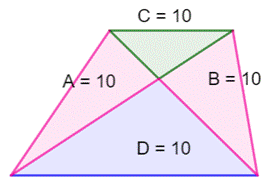
Définition Le trapèze est un quadrilatère possédant deux côtés parallèles. Propriété Le trapèze est partagé en quatre triangles par ses diagonales. Les deux triangles latéraux (A et B) ont la même aire. Leur produit (A.B = A² = B²) est égal au produit des aires des deux autres (C.D).		A = B A٠B = C٠D
Brèves associées	>>> Rectangle dans carré – Aire		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Trapèze		>>> Trapèze et pentagone

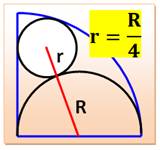
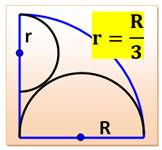
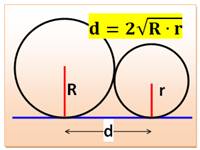
1089. Cercles tangents
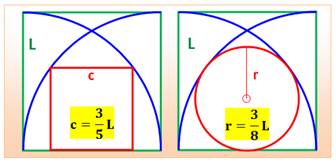
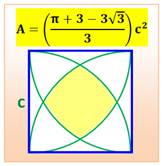
Relations typiques avec des cercles
Brèves associées	>>> Cercles tangents (3)	>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Défis géométriques avec cercles >>> Quarts de cercles	>>> Poster – Cercles >>> Cercles – Index

1090. Calcul mental de puissances
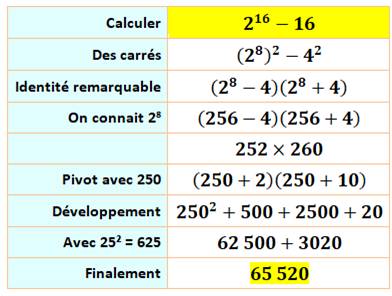
Méthode On demande à calculer cette expression: 2^16 – 16. Évidemment une calculette donne immédiatement 65 520. Certains, même, connaissent les puissances de 2 jusqu'à cette valeur: 2^16 = 65 536. Notez que l'on les retient facilement jusqu'à 10^10 = 1024, voire les suivantes 2048 et 4096. Calcul mental Ici, l'intérêt et de s'exercer à faire un calcul à la main et, ainsi, de s'exercer à la pratique des identités remarquables.
Brèves associées	>>> Calculer a^5 + b^5		>>> Brèves Calculs – Index
Pour en savoir plus	>>> Puissances de 2 >>> Nombre 65 536		>>> Identités remarquables >>> Calcul mental – Index

1091. Théorème de la bissectrice
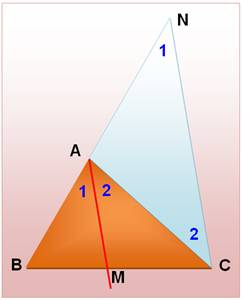
Propriété La bissectrice AM découpe une sécante BC dans le rapport des côtés adjacents AB et AC. Démonstration La démonstration est d'une grande simplicité à condition d'une petite astuce de tracé. On dessine NC parallèle à la bissectrice AM. Les angles A1 = N1 et A2 = C2 Or A1 = A2 (bissectrice). Conclusion: le triangle ANC est isocèle et AN = AC. Avec l'aide de Thales : Et en remplaçant AN par AC.
Brèves associées	>>> Bissectrices et cercle circonscrit	>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Bissectrice dans le triangle	>>> Théorème de Thalès

1092. Bissectrice & triangle rectangle
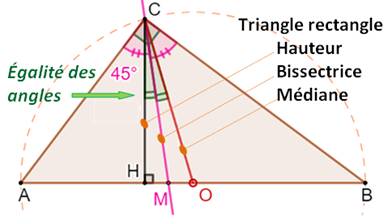
Théorème La bissectrice de l'angle droit du triangle rectangle est aussi la bissectrice de l'angle formé par la hauteur et la médiane. La démonstration est assez simple: comparaison des angles sachant que le triangle OBC est isocèle et que les angles non-droits du triangle rectangle sont complémentaires.
Brèves associées	>>> Angles dans trois carrés		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Bissectrice et triangle rectangle		>>> Bissectrice

1093. Théorème de Viviani
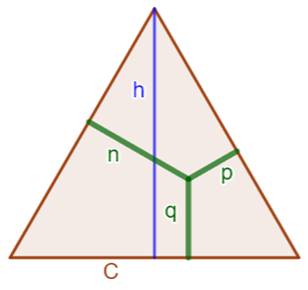
Théorème Dans un triangle équilatéral, la somme des distances d'un point intérieur quelconque aux côtés est égale à la longueur de la hauteur. Cette propriété se retrouve pour tous les polygones réguliers: Dans un polygone régulier, la somme des distances d'un point intérieur quelconque aux côtés, est constante; c'est celle obtenue en plaçant le point au centre du cercle inscrit.
Brèves associées	>>> Théorème de la carpette		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Théorème de Viviani		>>> Polygones réguliers

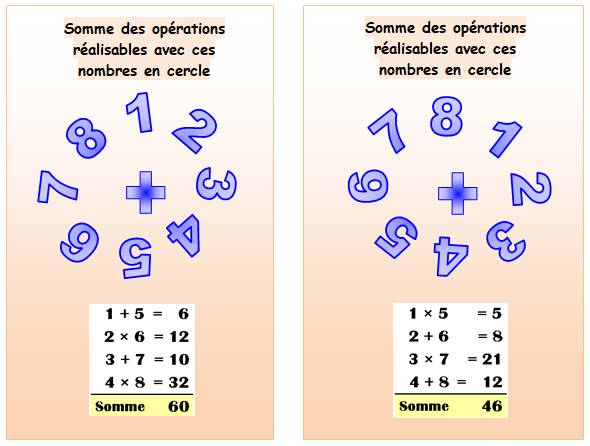
1094. Opérations en cercle
Brèves associées	>>> Somme des entiers	>>> Brèves Calculs – Index
Pour en savoir plus	>>> Calculs élémentaires – Index	>>> Nombres et jeux – Index

1095. Méthode Singapour
L'idée consiste à introduire des observations sans donner la procédure de calcul, laquelle sera expliquée dans un deuxième temps, après une bonne assimilation du procédé de comptage. Il s'agit essentiellement de visualiser les nombres, de les apprivoiser. On pratique les calculs avant d'analyser leurs principes. Analogie: l'enfant utilise automatiquement les verbes conjugués. Il apprend la grammaire et la conjugaison que bien après.		Étape concrète Comptage des bonbons.		Je compte 1, 2, 3, 4, 5, 6 bonbons
		Étape abstraite Addition des groupes de points.		2 + 2 + 2 = 6
		Introduction d'un nouveau concept Le signe multiplication.		3 × 2 = 6
Brèves associées	>>> Compter les chiffres		>>> Brèves Compter – Index
Pour en savoir plus	>>> Méthode Singapour		>>> Utilisation du boulier

1096. Nombres permutations
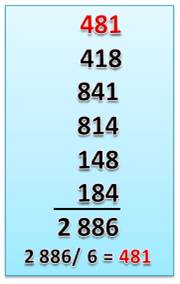
Présentation Un nombre permutation est tel qu'il est égal à la moyenne de la somme des permutations de ses chiffres; cad. somme des permutations divisée par la quantité de permutations. Les repdigits comme 111, 222, … sont naturellement de tels nombres. Le plus petit nombre permutation non repdigit est 370, suivi par 407, 481, … Propriété Ces nombres présentent tous cette forme comme pour 481 (un repunit divisé par3 ):		Exemples avec permutations circulaires (à gauche) et permutations complètes (à droite)
Brèves associées	>>> Nombres narcissiques		>>> Brèves Nombres – Index
Pour en savoir plus	>>> Nombres permutations		>>> Permutations >>> Repunit

1097. Énigme trompeuse !
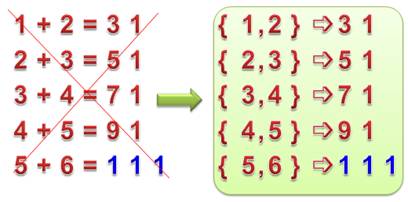
Tableau A Ce type d'énigme virale sur le Net, pourtant abordable dès l'école primaire, est néfaste pour nos enfants telle qu'elle est posée. Il s'agit de deviner le dernier nombre qui se trouve être 111. Tableau B Il serait préférable de ne pas perturber les jeunes esprits avec ce malencontreux signe égal. Le tableau B montre une disposition possible. La question devient alors: trouver l'opération rétablissant l'égalité. Tableau C Vous l'avez compris: la résolution consiste à imaginer l'opération (1 + 2) × 10 + 1 telle que présentée dans le tableau C.		Tableau A (mauvais) Tableau B (bon) Tableau C (solution)
Brèves associées	>>> Énigme du parking		>>> Brèves Énigmes – Index
Pour en savoir plus	>>> Énigmes virales sur le Net		>>> Énigme vicieuse

1098. Nombre premier record
Nombre premier Nombre divisible seulement par lui-même ou par 1. Comme: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31 … Il en existe une infinité comme démontré par le mathématicien grec Euclide il y a plus de 2 000 ans Nombre de Mersenne premier Nombre premier de la forme: 2^n – 1 et qui est premier. Comme: 2^3 – 1 = 7 et 7 est premier. Le suivant est: 2^5 – 1 = 31, ce nombre étant premier. Nombre de Mersenne premier record Nombre premier de Mersenne le plus grand. Le dernier connu remonte à 2018. Voir ci-contre. Parmi tous les types de nombres premiers ce sont les nombres de Mersenne qui battent actuellement les records. Les grands nombres premiers sont utilisés en cryptographie.		Le nombre premier record C'est le 51^e nombre de Mersenne. L'écriture de ce nombre nécessiterait un livre de 5000 pages avec fonte 11 (5000 caractères par page).
Brèves associées	>>> Nombre premier – Trouvez-le		>>> Brèves Nombres Premiers – Index
Pour en savoir plus	>>> Nombres premiers records >>> Nombres de Mersenne		>>> Barre magique des nombres premiers >>> Euclide – Biographie

1099. Centre de gravité du quadrilatère
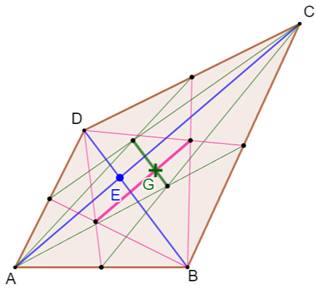
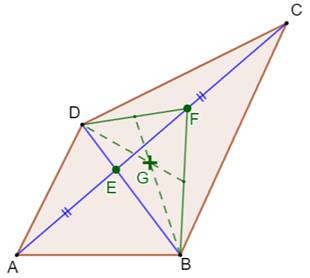
Construction classique du centre de gravité Quadrilatère ABCD et ses deux diagonales AC et BD (bleues); Centre de gravité des triangles ACD et ACB par tracé des médianes (en vert); segment qui relie ces deux points; Centre de gravité des triangles ABD et CBD par tracé des médianes (en rose); segment qui relie ces deux points; Le centre de gravité est le point de croisement de ses deux segments. Construction rapide du centre de gravité Quadrilatère ABCD et ses deux diagonales AC et BD (bleues); Segment FC de même longueur que AE; Triangle BDF; son centre de gravité est celui du quadrilatère; Médianes (en pointillés verts) qui se croisent en G; ce point est le centre de gravité du quadrilatère.
Brèves associées	>>> Quadrilatère – Centres de gravité		>>> Brèves Géométrie – Index
Pour en savoir plus	>>> Centre de gravité du quadrilatère		>>> Quadrilatère inscriptible

Retour	Brèves de maths – Page 54
Suite	Brèves de maths – Page 56
Voir	Voir liens en haut de page
Cette page	http://villemin.gerard.free.fr/NombDico/aBreves/Breve55.htm