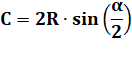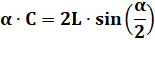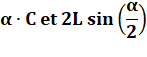|
Édition du: 18/04/2025 |
|
INDEX |
Cercles – Arc et corde |
||
Faites un double-clic pour un retour en haut de page
![]()
|
Arc et corde ➜ Rayon Connaissant la
longueur de l'arc et de la corde le sous-tendant, est-il possible de calculer
le rayon du cercle ? Oui, mais l'équation n'est pas simple à résoudre (transcendante). |
||
|
|
Sommaire de cette page >>> Résolution d'un exemple >>> Résolution par logiciels >>> Résolution avec tableur |
Débutants Glossaire |
|
Cas C = 5 et L = 5,5 Nous connaissons la longueur de la corde (C = 5) et celle de l'arc
sous-tendu (L = 5.5), calculez le rayon du cercle. C'est faisable car nous avons deux équations à deux inconnues. Le gros problème: nous obtenons alpha et son sinus dans l'équation. Le produit croisé et en simplifiant par R: Avec C = 5 et L = 5,5, la
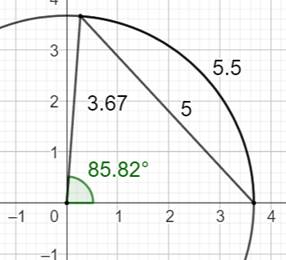
résolution de cette équation donne α = 1,49797328… rad =
85,8275470…° Et R = 3,671627562… |
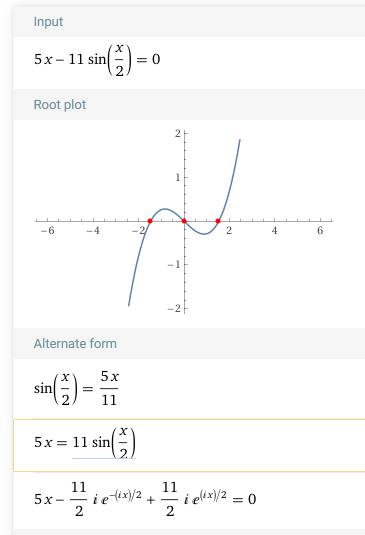
Résoution graphique
|
|
|
Maple Réinitialisation (restart). Introduction des valeurs de C et L. Écriture de l'équation. Demande de résolution (solve). Calcul du rayon R avec la première valeur [1] Le symbole % précise qu'il faut
prendre la valeur précédente. En bleu, le résultat des calculs Plus bas, un calcul de l'angle en degré. |
|
|
|
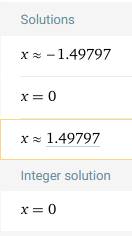
Ce calculateur en ligne est l'un des plus puissants accessibles sur
Internet. Il donne une solution détaillée avec les étapes de calcul. Ci-dessous la valeur de l'angle x en radian.
|
|
|
|
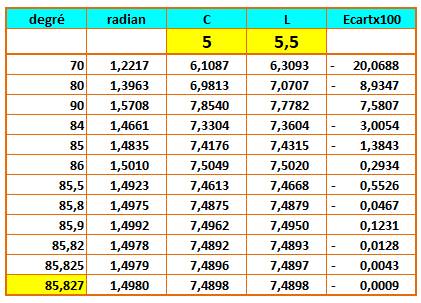
Il s'agit d'une résolution par approximations successives. Les colonnes avec en-tête jaune calculent respectivement: Ces deux valeurs sont comparées (colonne écart) pour approcher
l'égalité. |
|
|
Haut de page (ou
double-clic)
![]()