|
|||||||||||||||||||||||||||||||||
![]()
|
Les trois cercles de Monge Théorème de Monge / Théorème des
trois cercles Théorème relatif aux
tangentes à trois cercles dont la démonstration astucieuse de Monge recourt à
un passage en trois dimensions. Connu aussi par d'Alembert.
Gaspard Monge
(1746-1818), mathématicien français. Il est l'un des fondateurs de l'École
Polytechnique où il enseigne la géométrie. Il participe aussi à la fondation
de l'École d'arts et métiers. |
Voir Aire
du pentagone convexe quelconque
|
|
||
|
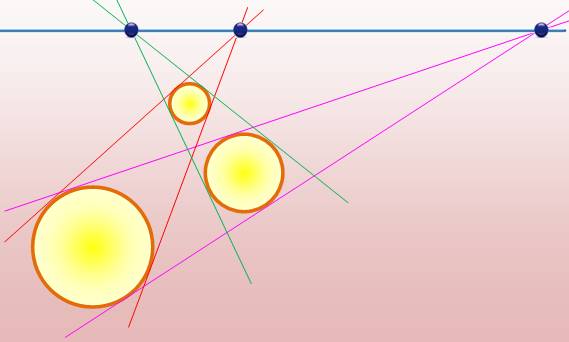
Trois
cercles de tailles différentes et dont les centres ne sont pas alignés. Les six
tangentes externes deux à deux. Alors, les trois points
d'intersection sont alignés. |
|
|
Anglais: Monge' Circle
Theorem
Autres théorèmes des trois cercles dus à Monge
(avec les cordes)
|
Lorsque trois cercles sont
sécants deux à deux, les trois droites d'intersection sont concourantes. Given three circles (in the same plane)
which pairwise intersect, then the three chords to which the points of
intersection give rise have a common intersection point. Si, deux cercles sont
sécants et que la droite commune passe par le point d'intersection d'une
sécante à l'un et d'une sécante à l'autre, alors, les quatre points
d'intersection sont cocycliques. |
|
|
||
|
Théorème
d'abord proposé par d'Alembert
(1717-1783). La
démonstration "3D" est due à Monge. Ce théorème est mentionné
dans le livre de David Wells sur les curiosités
géométriques. D'autres démonstrations sont
possibles utilisant:
Voir références |
||
|
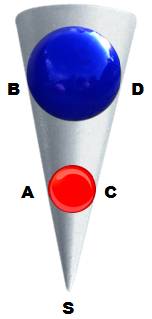
Démonstration de Monge Imaginons des sphères à la place des cercles.
Posées sur la table, elles sont tangentes à celle-ci. Imaginons trois cônes
(fins) qui enveloppent les sphères. Leurs sommets sont également sur la
table, car les deux points de tangence aux sphères et le sommet sont alignés. Pour les
trois cas, les points S1, A1, B1, S2, A2, B2, S3, A3, B3 appartiennent au
plan P de la table. Prenons maintenant, les points de tangence situés
de l'autre côté de la sphère: les points symétriques par rapport aux centres.
Eux aussi appartiennent au même plan Q contenant les sommets. (On peut
imaginer avoir figé le montage et le retourner sur la table) Les
points S1, C1, D1, S2, C2, D2, S3, C3, D3 appartiennent au plan Q. Appartenant aux deux plans P et Q, les trois
sommets S1, S2 et S3 appartiennent à leur intersection qui est une droite.
Ces trois points sont alignés. |
|
|
|
|
|
|
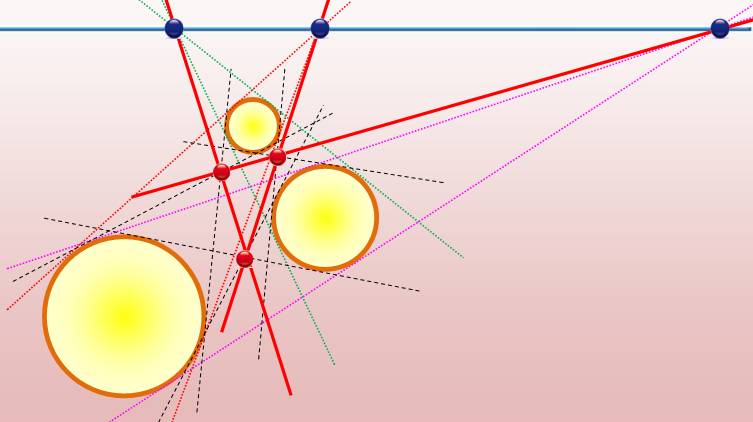
Les six
autres tangentes, les tangentes internes, se coupent en trois points. Ces
nouveaux points (rouges) sont alignés deux à deux avec l'un des trois points
précédents (bleus).
|
|
|
Quatre
sphères prises deux à deux et mise en cônes, tous les sommets étant du même
côté. Les sommets des six cônes se trouvent dans un même plan. |
![]()
|
Suite |
|
|
Voir |
|
|
DicoNombre |
|
|
|
|
|
|
|
|
Cette page |
![]()