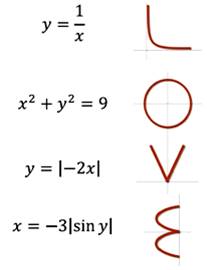|
||||||||||||||||||||||||||||
![]()
Citation
|
Les
douces courbes innombrables qui font d'un
corps de femme, pour l'homme qui en est amoureux, un paysage qu'il n'en finit
pas de découvrir et que chaque mouvement rend nouveau comme au jour de la
création. René Barjavel - Le Grand Secret
(1973) |
Voir Pensées et Humour
|
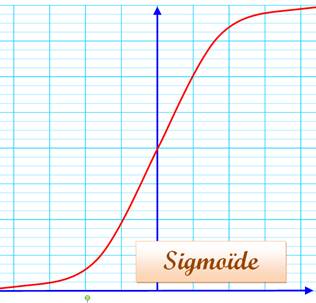
COURBES ÉLÉMENTAIRES Petit répertoire des courbes
les plus simples et idée de leurs usages. Les courbes classiques étudiées au lycée sont traitées sur d'autres
pages. Notamment: parabole, hyperbole, ellipse, logarithme, exponentielle. |
All you need is LOVE (Tu n'as besoin que d'amour
– Chanson des Beatles)
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
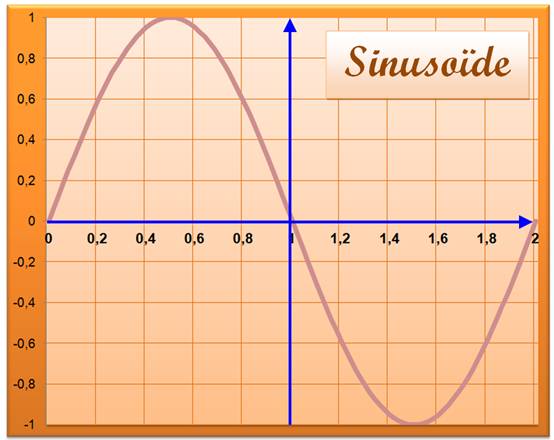
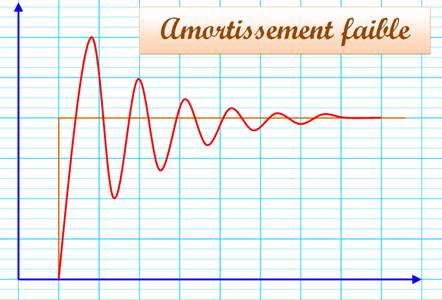
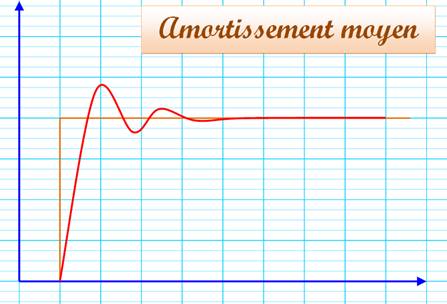
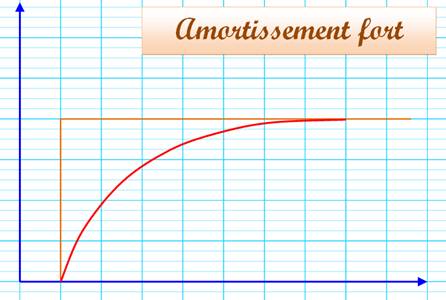
Voir
Trigonométrie / Électronique
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
Une courbe fermée sépare le plan en deux régions l'une, intérieure de la courbe, est
bornée l'autre, extérieure de la courbe, est infinie. C'est le théorème de
Jordan. Cela parait évident visuellement. Mais, très difficile à démontrer analytiquement. Formulation mathématique Toute courbe plane de Jordan sépare le plan R² en deux composantes
connexes disjointes dont elle est la frontière commune. L'une de ces
composantes est une partie bornée de R² appelée intérieure de la courbe.
L'autre composante est appelée l'extérieur de la courbe. Référence: Dictionnaire des mathématiques |
|
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
http://villemin.gerard.free.fr/Geometri/Courbes/CourbEle.htm
|
![]()