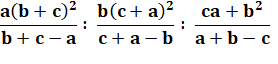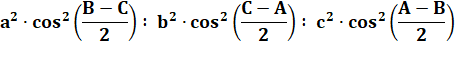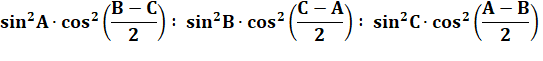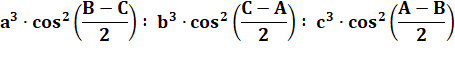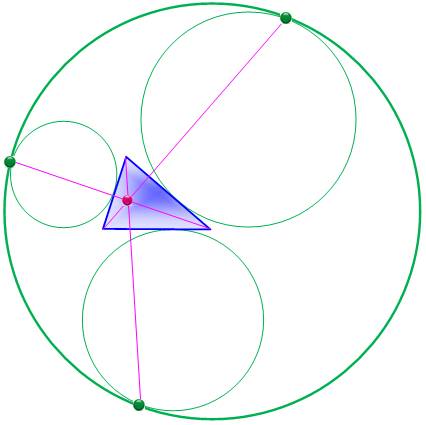
NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 07/01/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	CERCLE
Débutants Géométrie	TYPES			Glossaire Géométrie
INDEX Cercle Géométrie	Neufs points	Cercle d'Apollonius	Trois cercles d'Apollonius
	Autres types	Baderne d'Apollonius	Cercle numérique de Ducci
		Théorème de Descartes	Trois cercles de Monge
		Sommaire de cette page >>> Point et cercle d'Apollonius d'un triangle >>> Cercle d'Apollonius de deux points >>> Anglais

Point et cercle d'Apollonius d'un triangle			haut
Description Triangle bleu. Ses trois cercles exinscrits. Le cercle circonscrit à ses trois cercles: cercle d'Apollonius Les points de tangence. Les segments reliant ces points de tangence aux sommets du triangle d'origine Construction S'il est assez facile de construire les trois cercles exinscrits, il est beaucoup plus difficile de construire le cercle d'Apollonius. Voir Sites en références Propriétés Point X(181) de la nomenclature de Kimberling.
Coordonnées du point d'Apollonius	Trilinéaires: Barycentriques:

CERCLE D'APOLLONIUS de deux points
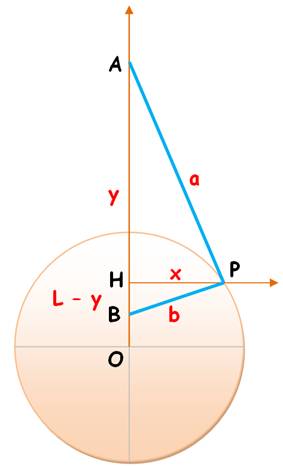
Soit deux points A et B et une constante k. Le lieu des points P tels que AP / PB = a / b = k est un cercle. Le cercle d'Apollonius des point A et B Si k = 1 le cercle devient une droite. Démonstration Nous cherchons: a/b = k a = k . b a² = k² . b² = K . b² Avec le système d'axes que nous avons construit et l'aide de Pythagore: a² = x² + y² b² = x² + (L – y)²	Lieu des point P tels que AP/PB = k ? Le cercle !
En reprenant l'expression de a² a² = k² . b² x² + y² = K (x² + (L – y)² ) = Kx² + K(L² – 2Ly + y²) = Kx² + KL² – 2 KLy + Ky² En mettant en facteur (1 – K)x² + (1 – K) y² + 2KLy – KL² = 0 Cette égalité est l'équation d'un cercle forme générique: x² + y² + 2fx + 2gy - c = 0 Constantes: f = 0; g = k² / (1 – x); c = k²L² / (1 – x) Coordonnées du centre (–f, –g) Rayon: r² = f² + g² – c

Anglais

Let O(A), O(B), O(C) be the excircles.

Apollonius's Problem includes the construction of the circle O tangent to the three excircles and encompassing them. The circle is called the Apollonius circle.

Let A' = O∩O(A), B'=O∩O(B), C'=O∩O(C). The lines AA', BB', CC' concur in X(181), the Apollonius point.

Voir Anglais pour le bac et pour les affaires

Suite	Trois cercles d'Apollonius et les 10 problèmes Puissance d'un point Apollonius
Voir	Cercle – Index Géométrie – Index
Sites	Problèmes d'Apollonius – Maths en folie Cercle et point d'Apollonius – Descartes et les mathématiques – Patrice Debart Problème des contacts – Wikipédia
Cette page	http://villemin.gerard.free.fr/GeomLAV/Cercle/Appollon.htm