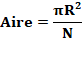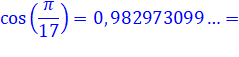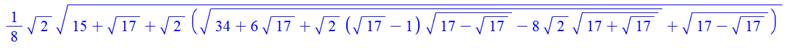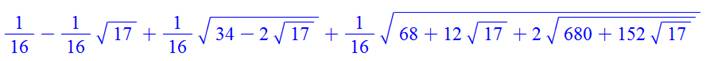|
|||||||||||||||||||||||||||||||||||||||||
![]()
|
Partage du cercle en n parties égales ou Construction du polygone
régulier à n côtés Partager en 2, 4 ou 8, c'est
relativement évident. Partager en 3, 6 ou 9, c'est un peu plus difficile. Partager en 5 fait partie
des constructions que l'on trouvaient dans les manuels de géométrie du XXe
siècle. Il existe des cas pour
lesquels il est impossible d'imaginer une construction géométrique à la règle
et au compas. >>> |
Voir DicoNombre pour
accéder aux nombres indiqués / Voir Polygone
index
|
Savez-vous
quelle est la meilleure façon de partager un gâteau pour en prendre une part
ou deux et remettre le reste au frigo? |
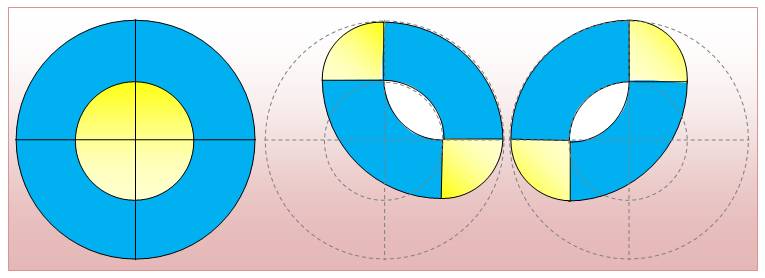
Comment partager un disque en deux anneaux
Voir Énigmes et puzzles
![]()
|
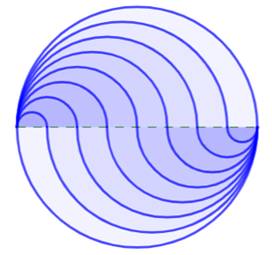
Problème Un
disque. Comment
obtenir N surfaces d'égales aires avec
règle et compas ? Solution Partager
le diamètre en N parties égales et tracer les demi-cercles comme pour cet
exemple (N = 8). Justification L'aire
de chaque demi-cercle est proportionnelle au carré du numéro du demi-cercle
de 1 à 8. On
calcule ce coefficient de proportionnalité
par différence entre la partie couverte et la partie en trop.
|
Disque partagé en huit surfaces d'égale aire
Chaque
surface (sorte de S) est composée de deux demi-cercles dont on retire deux
demi-cercles plus petits. L'aire
de chaque surface est égale à:
|
|
Voir Brève 51-1013
Pour information:
Calcul classique de l'aire (D = diamètre)
Premier calcul: D = 8; R = 4; aire du demi-cercle: ½ 𝛑R² = 8𝛑
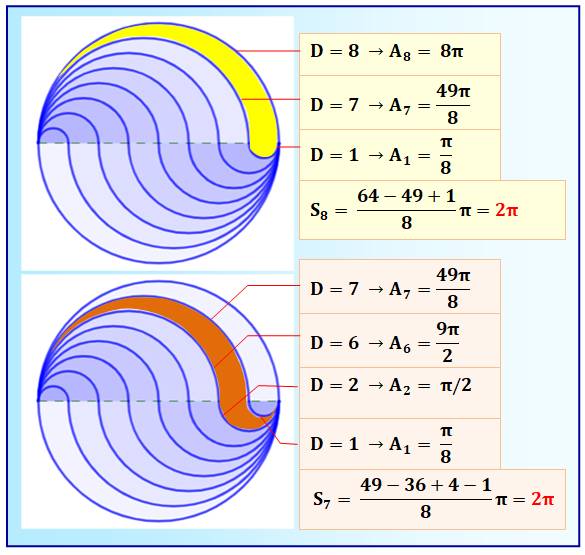
Aire du disque: 4²𝛑 = 16𝛑 et aussi: 8 × 2𝛑 = 16𝛑
![]()
Après
avoir partagé le disque, maintenant, on partage le cercle (la circonférence)
|
|
||
|
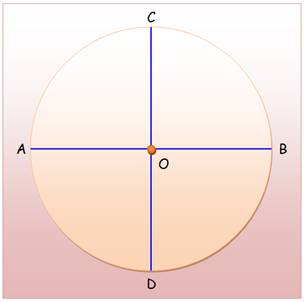
En
2
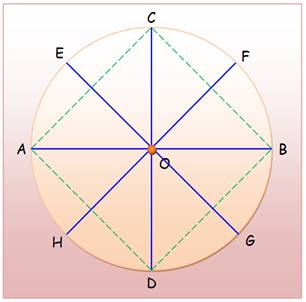
En
4
En
8 – méthode 1
En
16
|
|
|
|
|
||
|
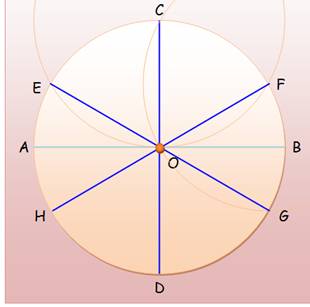
En
12 – méthode 1
Voir Sin 30° = 1/2 En
6 – méthode 1
En
3 – méthode 1
En
6 – méthode 2
Voir Rosace
/ Six en cercle En
3 – méthode 2
En
12 – méthode 2
|
|
|
Voir Partage
en 24, 48, 96 …
|
|
||
|
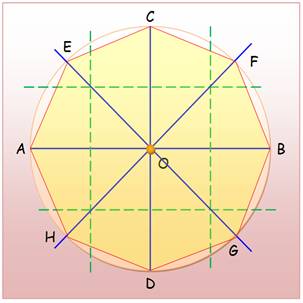
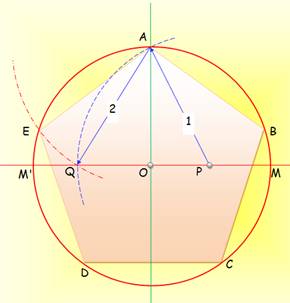
En
5
En
10 Prendre les
médiatrices des côtés du pentagone. En
15
Observation: Les
arcs délimités par le pentagone sont chacun divisés par 3 selon la
méthode vue lors du partage en 8. Note: Si vous dessiner sur avec un logiciel de dessin
ou avec Word, dessiner un pentagone, puis un deuxième que vous faire tourner
de 24° et un troisième avec rotation de 48°. |
|
|
|
|
||
|
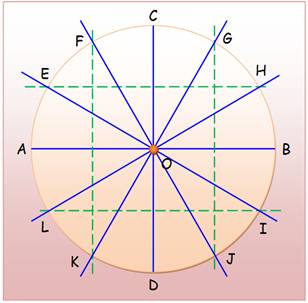
En
17
Voir Diaporama
par de Mélusine-Syracuse |
|
|
|
Valeur
du cosinus de l'angle Pi / 17 = 10,588235°
ou en simplifiant (un peu): Cette valeur exprimée avec radicaux provient de
la résolution d'une équation du huitième degré. Voir Angle Pi/17
et Heptadecagon
de Wolfram |
||
|
Question Savez-vous quelle est la meilleure façon de partager un
gâteau pour en prendre une part ou deux et remettre le reste au frigo? La solution fut présentée par Francis Galton en 1906: couper un gâteau rond selon des principes
scientifiques. Solution remise au goût du jour par Alex Bellos (vidéo sur
Numberphile: the scientific way to cut
a round cake >>>). Réponse |
|
|
Ce
qu'il ne faut pas faire: couper une
portion et remettre au frigo car les deux faces coupées vont prendre l'air et
rancir. |
|
|
Ce
qu'il faut faire: couper une section
centrale et rapprocher les deux "presque" demi-parts. Ainsi, les
faces coupées ne sont plus à l'air. Au besoin, maintenir avec un ruban élastique
autour du gâteau |
|
|
Pour
prendre une part le lendemain, coupez de la même façon mais en croix.
Rapprochez à nouveau les deux parts restantes. |
|
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()