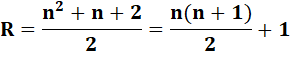|
|||||||||||||||||||||||||||||||||||||
![]()
|
Partage du cercle Cordes Divers types de problèmes
avec n points sur un cercle (par ordre de complexité): 1)
Compter les cordes >>> 2)
Compter les régions-cordes >>> (cette page) 2)
Compter les cordes qui ne se touchent pas >>> 3)
Compter les régions-points >>> Le
dénombrement, proposé ici, est simple à réaliser; nous allons voir comment
mettre nos observations en équation. |
|
|
||
|
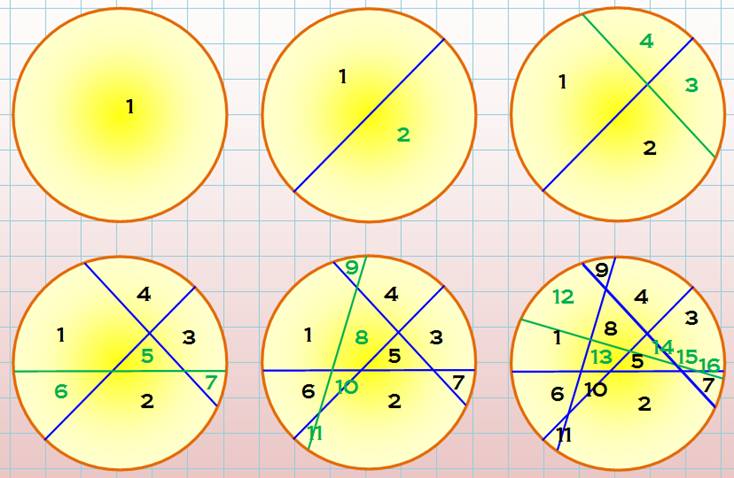
Il s'agit de compter les régions formées
par les cordes. Chaque corde coupe une fois et une fois
seulement toutes les autres.. Illustration pour 0 à 5 cordes
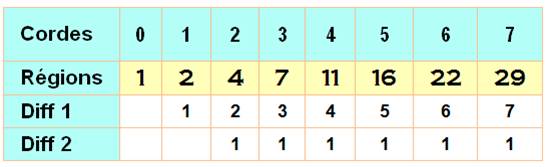
Tableau de dénombrement
La nième corde ajoute n régions. Formulation La différence seconde est constante. La
fonction qui donne la quantité de régions R en fonction de la quantité de
cordes n est du deuxième degré. Pour
fixer les trois coefficients, il faudra prendre trois cas de référence. |
||
|
Forme générale |
R =
an² + bn + c |
|
|
Pour n = 0, une région |
1 = 0
+ 0 + c |
|
|
Pour n = 1, deux régions |
2 = a
+ b + 1 |
|
|
Pour n = 2, quatre régions |
4 =
4a + 2b + 1 4 =
4a + 2(1 – a) + 1 4 =
4a + 2 – 2a + 1 2a =
1 b = 1
– a |
|
|
Formule donnant R régions en fonction de n
cordes. Soit, un en plus de la somme des entiers de 1
à n. |
|
|
|
Vérification pour n = 7 |
R7 = (7² + 7 + 2) / 2 = 58 / 2 =
29 |
|
Voir Différences secondes constantes
|
|
||
|
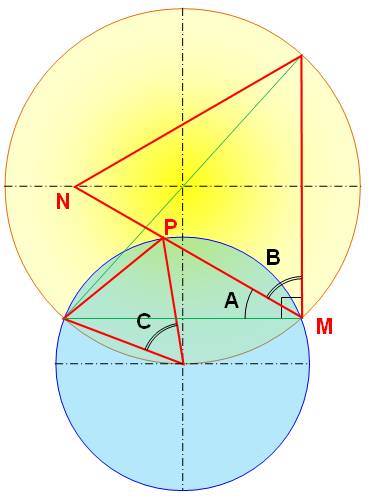
La figure Deux
cercles et deux triangles équilatéraux construits sur les cordes de la
manière indiquée. Propriété
remarquable quelle que soit la position du point M: P est
toujours sur MN. Démonstration Angles B et C = 60° dans les triangles
équilatéraux. Angle A + B = 90° avec le triangle inscrit ayant
un diamètre pour hypoténuse. Angle A, avec MN pour côté: 90 – 60 = 30° Angle A', avec MP pour côté: 1/2 de C = 30°, car
ils interceptent le même arc. Les angles A et A' sont égaux. Conclusion, MP et MN ont
la même orientation, les points M, P et N sont alignés. Le sommet P du petit
triangle est situé sur un des côtés du grand triangle. |
|
|
Voir Le
cheminement et la démonstration de Jean-Louis
Breuil, auteur de cette trouvaille
Voir Application à l'Octogone
et deux triangles équilatéraux
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()