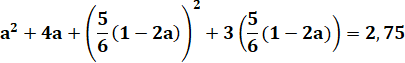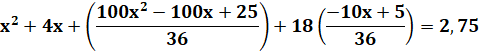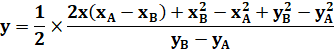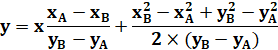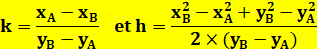le cercle et le calcul des coordonnées de son centre

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 01/02/2022 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	CERCLE
Débutants Géométrie	Propriétés				Glossaire Géométrie
INDEX Cercle Géométrie	Cercle	Propriétés	Équations	Théorèmes
	Centre	Fondements	Angles	Partage
	Orthogonaux
		Sommaire de cette page >>> Deux points du diamètre Deux points quelconques >>> Méthode équation du cercle >>> Méthode des médiatrices >>> Deux exemples de calcul des coordonnées du centre

Cercle passant par DEUX points

Coordonnées de son centre

Comment résoudre le cercle selon le minimum de connaissance que nous en avons. Notamment comment calculer les coordonnées du centre.

Ici, nous traitons le cas où le cercle passe par deux points.

Voir Construction du centre du cercle / Trouver le centre et le rayon du cercle – Introduction

Orientation: comment trouver les coordonnées du centre O

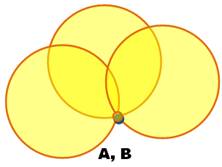
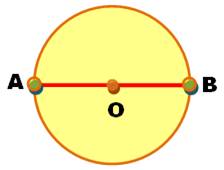
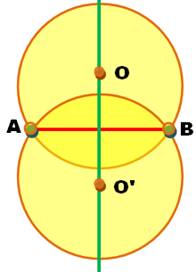
A et B confondus	AB = diamètre	A et B quelconques

Infinité de cercles	Un seul cercle	Deux cercles
Même pour un rayon donné	Rayon = AB / 2	Pour un rayon donné
Même pour un rayon donné	>>>	Méthode 1 >>> Méthode 2 >>>

Deux points, extrémités du diamètre

Données

Un cercle (jaune) qui passe par deux points donnés (A et B), extrémités d'un diamètre du cercle.

Questions

Tracez le centre du cercle.

Trouvez les coordonnées du centre.

Quelle est la longueur du rayon

Équation du cercle

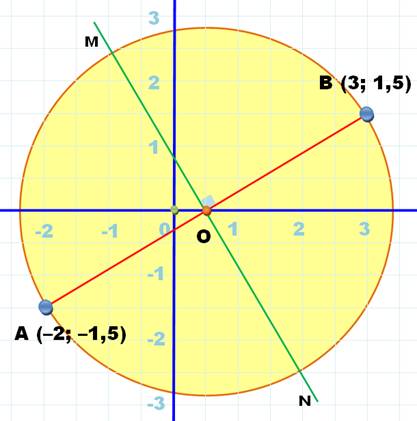
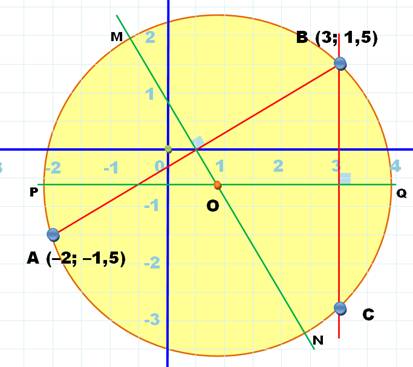
Tracé du centre du cercle

Dessinez le segment AB (rouge) et sa médiatrice MN verte).

Le point O est le centre du cercle.

Dessinez le cercle de rayon OA (jaune).

Coordonnées du centre

C'est la demi-somme de chaque coordonnée.

Diamètre du cercle

Avec le théorème de Pythagore.

Équation du cercle

À partir de l'équation générique.

(a et b) sont les coordonnées du centre

r est le rayon.

Vérification

Coordonnées du point à la verticale de B, abscisse 3.

Deux points quelconques et le rayon – Méthode par l'équation du cercle
Données Un cercle (jaune) qui passe par deux points donnés (A et B). Son rayon est connu (r = 3 unités). Questions Tracez le centre du cercle. Trouvez les coordonnées du centre. Trouvez les coordonnées du point C à la verticale de B. Tracé du centre du cercle Dessinez le segment AB et sa médiatrice MN. Dessinez le segment BC (C aurait pu être quelconque) et sa médiatrice. Le point d'intersection O est le centre du cercle. Il est à égale distance des ponts A, B et C.		La figure présente l'un des deux cercles possibles passant par A et B et de rayon = 3.
Coordonnées du centre du cercle L'équation générale du cercle comporte généralement trois inconnues (a, b et r).		(a et b) sont les coordonnées du centre r est le rayon qui est connu et égal à 3 unités.
Pour deux inconnues, il nous faut mettre en place deux équations. Une avec le point A et l'autre avec le point B.
Développement de ces expressions
Différence entre ces deux équations et déduction de la valeur de b.
Report de b dans la première équation
Calculs faits
Résolution pour a
Valeur de b
Équation des deux cercles possibles
Ordonnée du point C d'abscisse 3, sur le premier cercle.	y = –2,712677…
Note	La formulation analytique de la solution est bien trop compliquée. Sa programmation passe par les étapes vues ci-dessus.

Deux points quelconques et le rayon – Méthode par la médiatrice
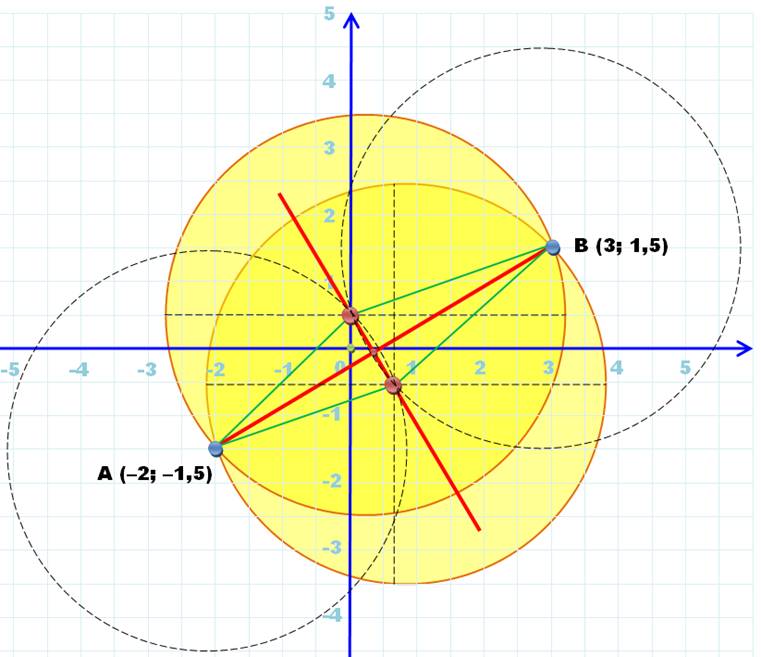
Problème Coordonnées du centre du cercle dont on sait qu'il passe par les deux ponts A et B et dont le rayon est connu. Commentaires La connaissance du rayon est nécessaire car par deux points passe une infinité de cercles. D'ailleurs, avec nos deux points, nous verrons que nous avons deux cercles de même rayon. Ce calcul est utile à ceux qui programment les machines-outils et qui utilisent l'interpolation circulaire. Illustration Deux points A et B de coordonnées: A = {-2; -1,5} et B = {3; 1,5}. Le rayon est : r = 3. Les deux cercles jaunes répondent à la question. Le centre de ces cercles se trouve sur la médiatrice du segment AB (rouge) Ces deux centres sont à la même distance r des points A et B (losange vert); ils sont à l'intersection des cercles de centre A et B et de rayon r (pointillés). Méthode Il suffit de donner l'équation des deux cercles pointillés et de trouver leur intersection. C'est-à-dire, résoudre un système d'équations à deux inconnues (x et y) L'équation du cercle étant une expression du second degré, deux jeux de solutions vont en découler. Le calcul littéral est fastidieux et complexe. Nous allons prendre l'exemple numérique de la figure. Calculs numériques
*Équation du cercle en A*
*Équation du cercle en B*
*Équations développées*
*Soustraction*
*Substitution*
*Solution: abscisses* Voir Résolution de l'équation du second degré
*Ordonnées*

Calculs algébriques
*Équation du cercle en A*
*Équation du cercle en B*
*Équations développées*
*Soustraction*
*On pose*
*Substitution*
*On pose*
*Solution: abscisses*
*Ordonnées*

Formules littérales	Cette formulation est très lourde! Je la donne pour en montrer la complexité.
*On pose*
*Valeur de x et x'*
*Valeur de y et y'*	(valeur développée encore plus complexe!)
*Formulation développée de x (reprenant les éléments ci-dessus)*