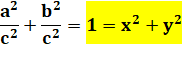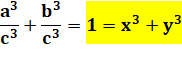|
|||||||||||||||||||||||||||||||||
![]()
|
RANG des COURBES ELLIPTIQUES Rang d'une courbe elliptique: nombre qui donne la quantité minimale de points rationnels qui
conduisent à la construction de tous les points
rationnels de la courbe. Cas du cercle: un seul point suffit pour trouver l'infinité
des points rationnels du cercle. Question: Existe-t-il une limite au rang des courbes
elliptiques? Une démonstration en vue: actualités 2018. |
|
|
||
|
Triplets de Pythagore Les triplets
de Pythagore peuvent se mettre sous la forme:
On sait que pour cette équation du
cercle de rayon unité, il existe une infinité de solutions pour x et y,
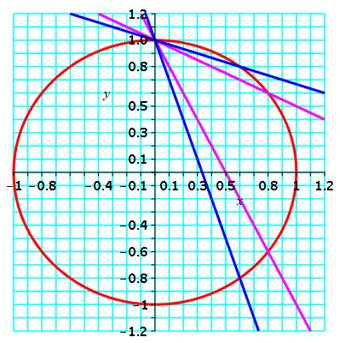
des nombres rationnels. Le graphe ci-contre illustre une propriété qui permet de trouver des
points rationnels sur une courbe à partir du moment où on en connait un.
Exemple: avec la droite:
y = 1 – 2x => intersection en
(0,8; -0,6) et (0,8)² + (-0,6)²
= 1 |
Cercle y² + x² = 1
Droites magenta: y = 1 – x/2 et y = 1 – 2x Droites bleues: y = 1 – x/3 et y = 1 – 3x |
|
|
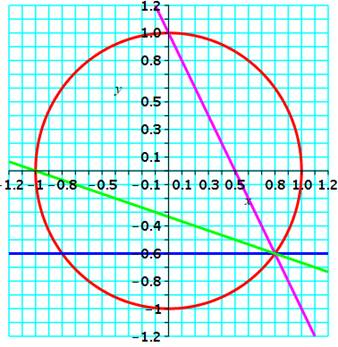
Infinité de points rationnels La méthode de construction des points rationnels
peut être appliquée aux nouveaux point rationnels. Les droites bleue et verte, construites à partir
de l'intersection de la droite magenta,
illustrent cette propriété. Ici, la construction peut se répéter à l'infini
du fait qu'il existe une infinité de triplets de Pythagore. Ce qui est important pour le cercle: en partant
d'un seul point, il est possible de trouver tous les points rationnels du
cercle. Mais, ce
n'est pas toujours le cas. Alors combien faut-il de points de départ pour
trouver tous les points rationnels de la courbe ? |
Propagation des points rationnels
La droite magenta coupe le cercle en deux points
rationnels. À partir de l'un d'eux,
les droites à pente rationnelle coupent également le cercle en des points
rationnels. |
|
|
Triplets de Fermat-Wiles Le théorème
de Fermat-Wiles affirme que: an + bn = cn n'a pas
de solution en nombres entiers pour n > 2. |
Ce qui revient à dire, par exemple:
Cette équation, n'a pas de solution en nombres
rationnels positifs: a/c et b/c. |
|
|
|
||||
|
Rang d'une courbe Le rang est la
quantité de points rationnels indépendants permettant de trouver tous les
points rationnels de la courbe. C'est un invariant qui caractérise la courbe. Théorème de Mordel (1922) Pour une courbe elliptique, il existe un ensemble fini de points
rationnels tel que tout point rationnel de la courbe s'obtienne à partir de
ces points par un nombre fini d'applications de la méthode de la sécante ou de la tangente. Le
rang est le cardinal
de cet ensemble. |
Le cercle est de rang 1,
Rang nul Les courbes elliptiques qui n’ont qu’un nombre fini de points
rationnels sont de rang 0. |
|||
|
Courbes elliptiques Leur équation: y2 = x3 +
Ax+ B Leur cas est intéressant car elles sont l'étape après les cercles (passage du degré
2 au degré 3). Ce sont les courbes les plus compliquées pour lesquelles les
mathématiciens ont une certaine maitrise. (Note: Ces sont les courbes
non-rationnelles les plus simples). La limite de la quantité de points de départ pour
couvrir tous les points rationnels des courbes elliptiques n'est pas connue.
La connaissance du rang des courbes elliptiques est une question ouverte. Le rang des courbes elliptiques Le rang est une indication de la complexité de la courbe: plus il est
élevé, plus l’ensemble des solutions rationnelles de la courbe est vaste et
complexe. Il est très difficile à calculer. |
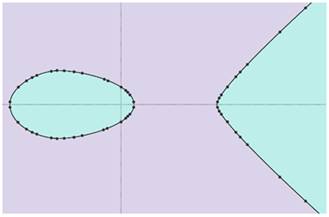
Les points rationnels de y2
= x3 – 4x + 1
Source Kevin
Hartnett Note: La courbe
est constituée de deux morceaux, de deux composantes
connexes. |
|||
|
D'une manière théorique Aucune méthode ne permet actuellement de déduire le rang à partir de
la fonction représentant la courbe. Un simple changement de coefficient et le
rang est modifié, et parfois très notablement. |
Limite ou pas limite ? Les mathématiciens pensaient qu'il y avait une
limite au rang d’une équation algébrique. Dans, les années 1970, la plupart des
mathématiciens en sont venus à penser que le rang n'est pas borné, ce qui
signifie qu'il devrait être possible de trouver des courbes algébriques ayant
un rang arbitrairement élevé. En 2018, le balancier repart vers l'existence
d'une limite. |
|||
Exemples
|
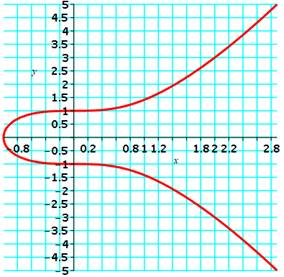
y2 = x3 + 1
Points rationnels: 5 Rang: 0 |
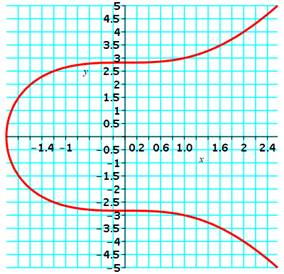
y2 = x3 + 8
Points rationnels: infinité Rang: 1 |
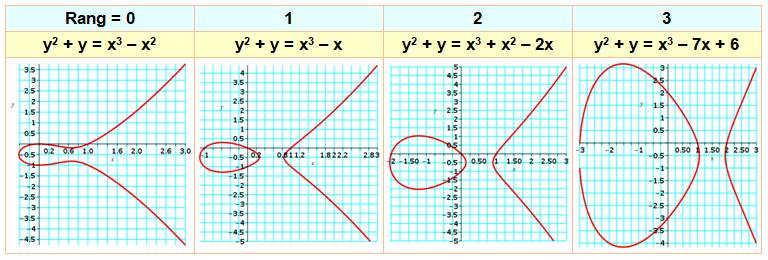
Les
quatre courbes les plus simples de rang 0 à 3
|
|
||
|
Dorian Goldfefd En 1979, il conjecture que globalement, la moitié des courbes
elliptiques sont de rang 0 et l'autre moitié de rang 1. De fait, elles
sont très majoritaires, mais il en existe "un peu" de rang supérieur. Noam Elkies (Harvard). Il détient le record d'une courbe elliptique de rang 28, découverte en
2006. Andrew Granville En 2008, trouve qu'au-delà du rang 21, il y a un nombre limité de
courbes elliptiques de rang supérieur. Manjul Bhargava
et Arul Shankar En 2010, ils établissent ce théorème: Lorsque les courbes elliptiques sont ordonnées par hauteur, leur rang
moyen est au plus égal à 1,5. Jennifer
Park, Bjorn Poonen and Melanie Wood, John Voight (Ohio) En 2018, cette équipe suggère qu'il existe une limite et, en fait,
elle ne serait pas très grande. Ils confirment que: Il n'y a qu’un nombre fini de courbes elliptiques ayant un rang
supérieur à 21. L'une d'entre-elles doit donc forcément avoir le rang le plus
élevé dans le lot, ce qui signifie que le rang est borné. |
Modélisation L'équipe de Jennifer Park utilise un modèle qui
ressemble aux courbes elliptiques: les
noyaux de certaines matrices définies sur des corps fini. Plus faciles à étudier. La distribution des dimensions du noyau est
supposée proche celles des rangs des courbes elliptiques. Cette supposition n'est pas gratuite. Tous les
travaux effectués avec ce modèle se sont avérés fructueux, avec, à la clé,
même quelques preuves. Familles de courbes elliptiques On a montré que pour beaucoup de familles, le
rang est borné. Une bonne piste pour corroborer les conclusions de 2018. Point final? Noam Elkies prétend sagement que le domaine n'est
pas assez connu pour conjecture une limite ou non. Un défi toujours vivant … |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
![]()