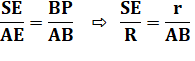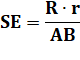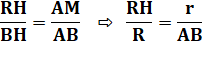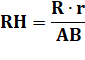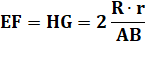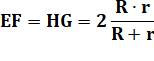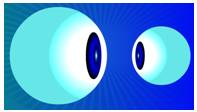
NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 13/10/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	CERCLE
Débutants Géométrie	CERCLES INSCRITS …				Glossaire Géométrie
INDEX Cercles Triangles	Index	Inscrit	SANGAKUS	Deux cercles – Triangle
	Introduction	Inscrit (suite)	Jumeaux	Deux cercles – Carré
	Puissance	Circonscrit	Carré max	Trois cercles – Construction
		Exinscrits	Face à face	Trois cercles – Tr. Équilatéraux
				Quatre cercles – Construction
		Sommaire de cette page >>> Théorème du face à face >>> Démonstration >>> Variante 1 >>> Variante 2 >>> Avec trois cercles >>> Généralisation

Les deux cercles en face à face

Eyeball theorem

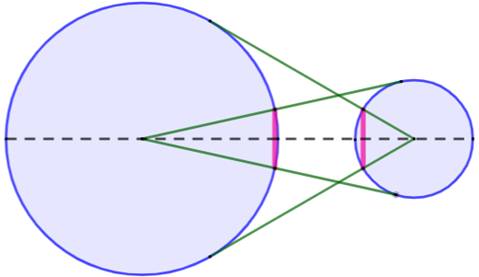
Deux cercles quelconques et leurs tangentes issues du centre de chacun. Les cordes interceptées sont égales (isométriques).

Théorème du face à face
Deux cercles quelconques. Les tangentes issues du centre des cercles. Les cordes (roses) sont égales. Valable pour deux sphères avec deux cercles égaux (en rouge). La figure ressemble à deux yeux qui se font face. D'où le nom en anglais: eyeball theorem, pour théorème des globes oculaires ou théorème des quinquets.

Démonstration
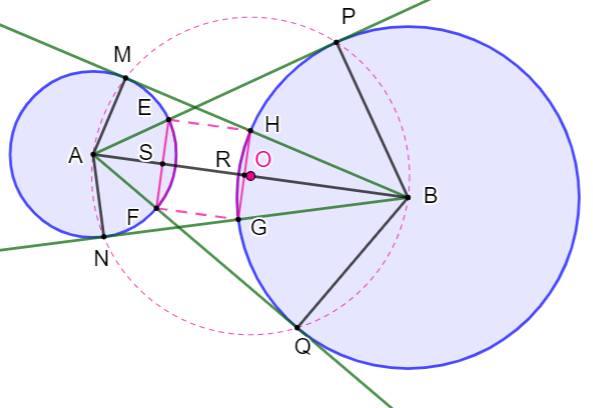
Du côté du cercle de gauche Les tangentes sont symétriques par rapport à AB. S sur AB est le milieu de EF. Triangle ASE: rectangle Triangles ASE et APB rectangles et l'angle en A est commun: ils sont semblables.
Même chose à droite R sur AB est le milieu de HG. Triangle BRH: rectangle Triangles BRH et BMA rectangles et l'angle en B est commun: ils sont semblables. Note: les droites EF et HG sont perpendiculaires à AB, elles son parallèles.
Conclusion Les cordes sont égales
En cas de tangence Si les deux cercles sont tangents, alors AB = R + r		Moyenne harmonique des rayons
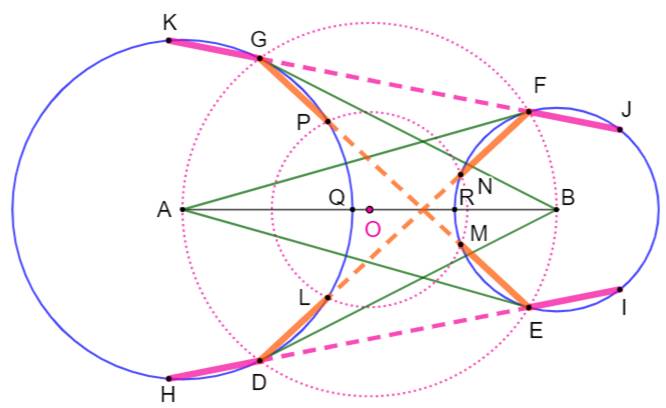
Théorème Deux cercles et les tangentes issues du centre du cercle opposé. Les cordes interceptées par les tangentes sont égales et parallèles. Ce sont les côtés d'un rectangle.	Le quadrilatère EFGH est un rectangle. Du fait des triangles rectangles avec même hypoténuse, les quatre points de tangence et les deux centres sont cocycliques.

Variante 1
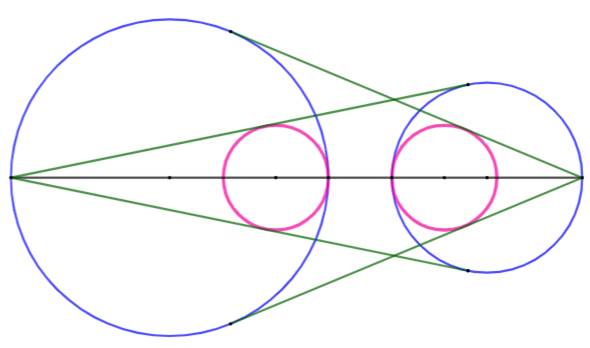
Description Deux cercles bleus (A) et (B). Les tangentes (vertes) issues des centres. Segments rejoignant les intersections deux à deux: GF, DE, GE et DF. Prolongés et intersections avec les deux cercles: H, I, J, K.	Théorème Les cordes découpées sur les cercles forment deux fois quatre segments égaux. KG = FJ = HD = EI GP = ME = DL = NF

Variante 2
Description Deux cercles bleus. Les tangentes (vertes) issues des points les plus éloignés (en non plus les centres).	Théorème Les cercles inscrits (tangent au cercle et aux droites tangentes) sont isométriques.) Les deux cercles roses sont identiques.

Avec trois cercles
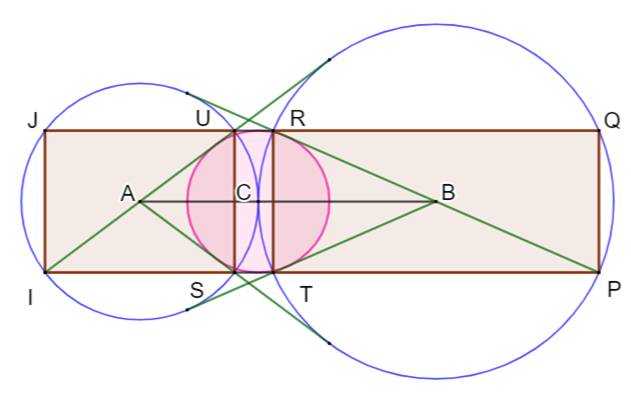
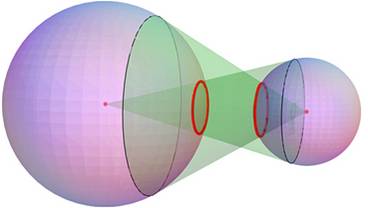
Description Deux cercles bleus (A) et (B), tangents en C. Un cercle (C) rose, de rayon quelconque inférieur à AC et BC. Les quatre tangentes (vertes) issues du centre du cercle opposé. Intersections J, U, R, Q, I, S, T, P.	Théorème Les trois quadrilatères sont des rectangles alignés (J, U R, Q sont alignés). Les droites JQ et IP sont tangentes au cercle (C).

Généralisation 3D

Les deux cercles rouges sont congruents

Suite	Sangakus Rayon du cercle circonscrit Cercle inscrit Puissance d'un point par rapport à un cercle
Voir	Bissectrices Cercle – Index Cercles et triangles Cône	Diamètre Géométrie – Vocabulaire Périmètre Sphère
Sites	Le théorème Eyeball – M@yhs et tiques The Eyeball Theorem – Cut-the-Knot – Six démonstrations et quantité de variations sur ce théorème Praying Eyes Theorem – Cut-the-Knot Eyeball Theorem – Wolfram MathWorld An Eye on Eyeball – Prithwijit De The Eyeball Theorem generalized – mathoverflow
Cette page	http://villemin.gerard.free.fr/GeomLAV/Cercle/FaceFace.htm