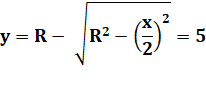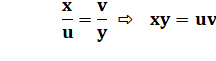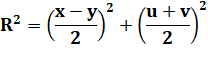|
||||||||||||||||||||||||||||||||||||||||
![]()
|
CERCLE – Fondements
|
|
|
|
|
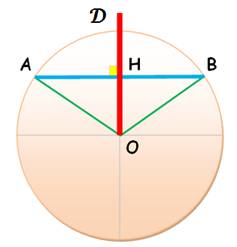
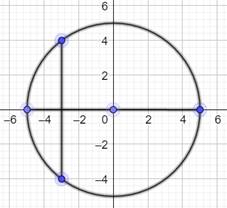
Sécante
Formalisation
mathématique de cette propriété (pour l'exemple): Soit 𝓓 une droite du plan affine euclidien, C un cercle de centre O et de rayon R, et Si d(O,𝓓) < R, on a card (Ω) = 2.
Diamètre
Rayon
et centre
Corde
|
|
|
Symétrie
Deux,
trois et quatre points
Deux
cercles (ou plus)
|
|
|
|||
|
Théorème
La réciproque est
vraie: La médiatrice d'une
corde passe par le centre du cercle. |
|
||
|
Hypothèses
Théorème invoqué
|
Démonstration
|
||
Note: il est recommandé de présenter une
démonstration systématiquement de la manière indiquée ci-dessus,
à la mode de la classe de cinquième!
Du moins, il y quelques années …
|
|
||
|
La sagitta ou flèche (y) est la portion de diamètre situé entre
la corde et le cercle. Exemple de calcul du rayon
Autres formules
|
|
|
Voir Développements en Arcs, cordes
et sagittas
|
|
|||
|
Théorème
Conséquence Un cercle est
complètement défini par trois points. |
|
||
|
Hypothèses
Théorème invoqué
|
Démonstration
|
||
|
|
||
|
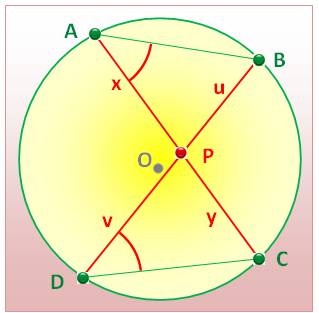
Théorème des cordes Les diagonales d'un quadrilatère cocyclique se
coupent selon la relation: xy = uv ou équivalent Deux sécantes passant par un point P du cercle,
se coupent selon la relation: xy = uv ou encore La puissance
d'un point par rapport à un cercle est constante quelle que soit la corde
choisie. The
power of a point with respect to a given circle is constant. Démonstration 1 (figure du haut) les angles à gauche marqués en rouge interceptent
le même arc, ils sont égaux. Idem à droite. Les triangles APB et DPC sont semblables
et les mesures des côtés sont proportionnelles:
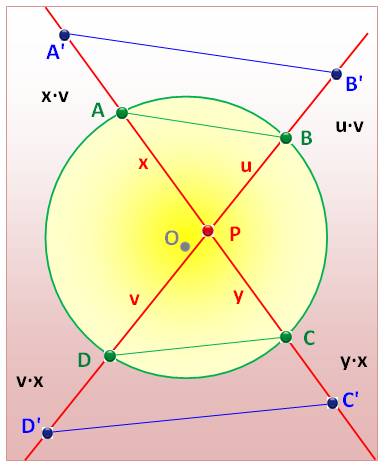
Démonstration 2 (figure du bas) Une belle démonstration pour le plaisir On trace le triangle A'PB' homothétique de APB dans le
rapport v. On trace le triangle C'PD' homothétique de CDP
dans le rapport x. De sorte que A'P = D'P = vx On va montrer qu'il en est de même à droite. Les quatre angles à gauche sont égaux:
interception du même arc, et effet d'homothétie. Idem pour ceux de droite. Les quatre triangles sont semblables car trois
angles égaux. Les grands triangles A'B'P et C'D'P sont
semblables avec deux côtés égaux à gauche; ces deux triangles sont égaux et
les deux côtés de droite sont égaux: |
|
|
Voir Puissance
d'un point / Calculs avec ce théorème / Brève 63-1259
|
|
||
|
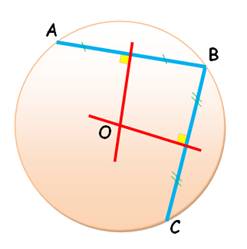
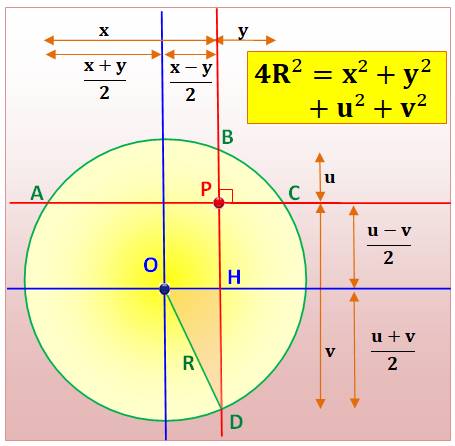
Théorème des cordes Deux cordes perpendiculaires sont telles que. 4R²
= x² + y² + u² + v² Démonstration On trace les médiatrices
(bleues) des cordes AC et BD. Le centre du cercle se situe à leur
intersection La figure montre le calcul des dimensions dont
celles du triangle
rectangle OHD, et avec Pythagore:
Or, les
cordes, orthogonales
ou non, se coupent avec la relation: xy = uv Soit la relation cherchée en 4R². |
|
|
|
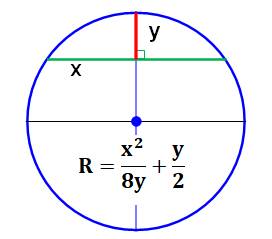
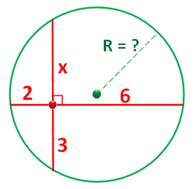
Problème classique Avec ces trois mesures, retrouvez le rayon du
cercle. Théorème des cordes: Relation donnant le rayon: |
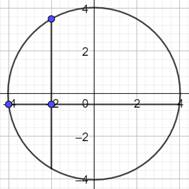
Figure de l'énoncé et figure de la solution
|
|
|
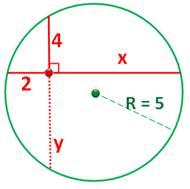
Du même type … Quelle est la longueur de la corde ? On ne connait que les deux longueurs 2 et 4 et
aussi le rayon 5 On prolonge le segment 4 (pointillés). Théorème des cordes: Relation donnant le rayon: Longueur de la corde: 2 + 8 = 10. |
|
|
Merci à Jean-Marc Detourmignies pour ses
conseils
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette
page |
![]()