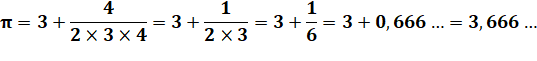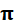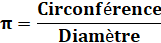|
||||||||||||||||||||||||||||||||||||||||
|
Constante Pi ( Page dédiée aux débutants
juniors Je ne suis pas débutant >>>
Constante Pi:
nombre
spécial compris entre 3 et 4. Impossible de le représenter par une fraction. Son écriture avec des décimales ne s'arrête
jamais. Mais à quoi correspond un tel nombre?
Pourquoi en avons-nous besoin? |
|
Cette page n'est pas un cours (comme d'ailleurs
toutes les pages
de ce site) ! Son contenu reflète les trucs utilisés par l'auteur pour
encrer durablement les notions de périmètre du
cercle et d'aire du disque à des
enfants en accompagnement particulier. Les encarts ludiques favorisent
l'attention et la mémorisation.
|
|
Pirouettes et autres pitreries Bébé, je fais pipi
n'importe où; je pisse en lit … À la ferme, j'ai vu beaucoup de pis; et les vaches m'épient!
La paille a des épis;
et pis après? Les pies sont
voleuses! Qui copient-elles? Pi rate, pi se tache
et pire encore. Auteur inconnu - Voir Pensées
& humour |
Pis
vert en verre Lettre grecque
Pi coloriée en vert Oiseau
commun: le pic vert Voir
Rébus |
|
Pape de 1939 à
1958, notamment au moment de la seconde guerre mondiale. Position difficile
face aux nazis d'Hitler et aux fascistes de Mussolini. Les enfants s'amusent plutôt avec Pie VII (1742-1823).
Voir
Histoire |
|
|
|||
|
J'enroule une bande autour de la roue de mon vélo
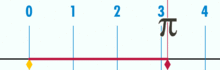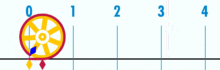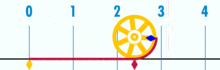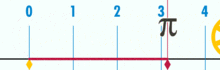
dont le diamètre est 1 m. Je la déroule et la pose au sol. Je mesure sa longueur. Je constate que la bande au sol mesure un peu plus
de 3 m. En fait, une mesure soigneuse montre que c'est 3,14 m. Le périmètre d'un cercle de diamètre unité est
Pi. = 3,14… |
|
||
|
Je sais maintenant
qu'en un tour, la valve rouge "fait Pipi".
Avec cette image en
tête, je retiens que:
Cette relation
sera très utile en trigonométrie.
|
Attention,
sur la route, la roue avance seulement de Pi.
|
||
|
Avec le diamètre Le nombre Pi correspond à la longueur du cercle
lorsque que le diamètre vaut une unité. Le rapport (la fraction) circonférence sur
diamètre vaut Pi pour tous les cercles. Il est noté avec la lettre grecque Avec le rayon Le nombre Pi correspond à la longueur d'un demi-cercle
lorsque que le rayon vaut une unité. |
|
||
Voir Cycloïde
|
|
||
|
Le grand carré en rose a un
côté qui mesure D mètres. Son périmètre est égal à 4D. Le périmètre du cercle (on
dit aussi circonférence) est plus petit que le périmètre du grand carré.
C'est là qu'intervient Pi. Le périmètre du cercle est
plus petit que 4D, il mesure 3,14… D La circonférence divisée par le diamètre donne la valeur de Pi. En prenant le rayon, le
périmètre du cercle est égal à: P = 3,14… x (2R) = 2 x 3,14… x R P = 2 |
Périmètre du carré = 2 x
4 x R Périmètre du cercle = 2 x 3,14 … x R |
|
|
|
||
|
L'aire du grand carré est
égale à D² ou 4 fois les petits carrés violets, soit 4R² L'aire du disque est plus
petite. Elle vaut A = 3,14… R² = Avec le diamètre: A = 3,14… (D/2)² = 3,14… x D² / 4
|
Aire du carré = 4 x R² Aire du disque = 3,14… x R² |
|
Bilan
(les formules avec le rayon sont à retenir par cœur)
Citations
|
Les
travaux théoriques ou pratiques portant sur ce nombre sont un voyage
vers l’infini plein de surprises et
d’émerveillement. A
partir d’Archimède, Pi existe comme
un objet mathématique parfait et inaccessible et, de ce fait, comme défi
permanent à l’intelligence des
hommes. Jean-Paul Delahaye. |
|
|
||
|
La valeur courante pour les
applications simples est la suivante: |
|
|
|
Avec un peu plus de
décimales: |
|
|
|
Avec vingt décimales |
|
|
|
Pi est une valeur un peu
plus grande que 3. De combien approximativement? |
|
|
|
Encore mieux (six décimales
exactes) |
|
|
Les vingt premières décimales de Pi arrangées le long d'un
cercle de diamètre unité
Représentation
artistique représentant PI comme la
circonférence d'un cercle de diamètre unité
|
|
|
|
Une des formules qui permet de calculer Pi. Formule de
l'Indien Nilakantha
(1444–1544). Plus on calcule de fractions
et plus on se rapproche de la valeur de Pi.
Essayons de calculer les
premiers termes. Ce ne sont que des fractions après
tout.
Les trois petits points
indiquent qu'il existe d'autres décimales. Ici, ce sont
des 6 sans arrêt (une infinité). Le tableau montre les
calculs pour les fractions suivantes. En rouge, les décimales exactes du
nombre Pi. Note: Le "rang"
indiqué est en fait le premier nombre en dénominateur de la fraction. Ce tableau montre que cette
formule conduit progressivement vers la valeur de Pi, mais très, très
lentement. Avec 5 000 fractions (calculées avec un ordinateur), le résultat
approche Pi avec seulement 11 décimales. |
|
Merci à Pierre Germain-Lacour pour ses remarques pertinentes
|
Pi
( La
calculette
de votre ordinateur en mode scientifique donne 31 décimales. Ce nombre est essentiellement la mesure de la circonférence
d'un cercle de diamètre
égal à 1. Ou plus généralement pour tous les cercles, Pi est le rapport de leur
circonférence à leur diamètre:
La
constante Pi se retrouve dans pratiquement tous les domaines mathématiques
traitant de ce qui est courbe ou ondulant.
On la découvre également en probabilité.
Cette constante est universelle, d'où
l'importance que tous les mathématiciens lui accorde. Certains, par pur
passion, cherche à en connaître le maximum de
décimales (des milliers de milliards!).
|
|
Suite |
|
|
Voir |
|
|
Cette page |
