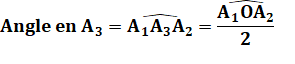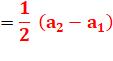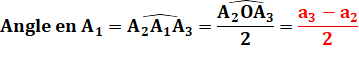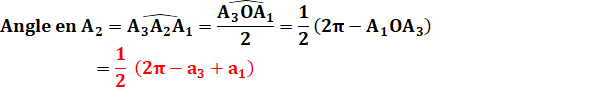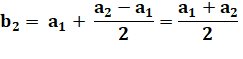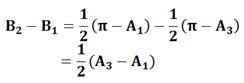NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 31/03/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	CERCLE
Débutants Général	Propriétés			Glossaire Général
INDEX Cercle	Propriétés	Équations	Théorèmes
	Fondements	Angles	Partage
	Sécante	Tangente	Sécantes et tangentes
			Arcs, cordes et sagittas
		Sommaire de cette page >>> Propriétés fondamentales >>> Angles intérieurs >>> Angle au centre et angle inscrit >>> Polygones réguliers >>> Triangle dans le cercle et abscisses angulaires >>> Le parallélogramme >>> Angles du triangle conjugué

Angles dans le cercle

Théorème de l'angle inscrit

Propriétés des angles inscrits et angles au centre dans un cercle. Relations en utilisant les abscisses angulaires.

Itération de triangles inscrits dans un cercle telle que ces triangles convergent vers une forme équilatérale.

Propriétés fondamentales

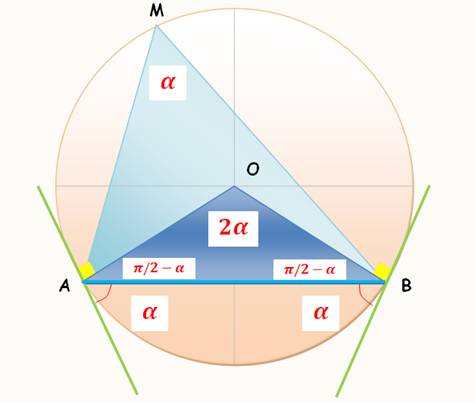
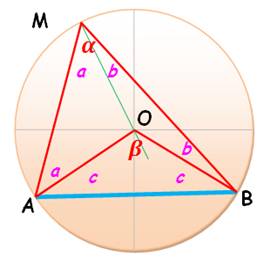
Relations entre les angles dans un cercle Commentaires Une corde AB quelconque; l'angle inscrit AMB vaut Alors l'angle au centre AOB vaut 2 L'angle au centre vaut deux fois l'angle inscrit interceptant le même arc. Les angles formés avec le segment AB et les tangentes au cercle en A et B valent . Notez que les rayons OA et OB sont perpendiculaires à la tangente en A et en B. Or, les angles à la base du triangle isocèle valent: ½ ( – 2) = /2 – D'où la valeur de l'angle avec les tangentes.

Voir Triangles dans le cercle / Angle inscrit et angle au centre

Angles intérieurs constants
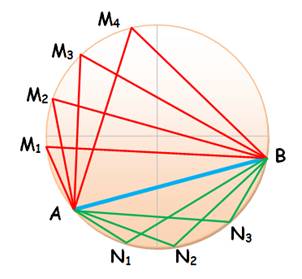
Les angles en M sont égaux A M1 B = A M2 B = A M3 B = A M4 B Les angles en N sont égaux A N1 B = A N2 B = A N3 B Les angles en M et N sont liés A M1 B + A N1 B = Ces angles sont supplémentaires	Les angles qui interceptent une même corde sont égaux. Cet angle vaut la moitié de l'angle au centre interceptant le même segment. Voir Démo / Polygone
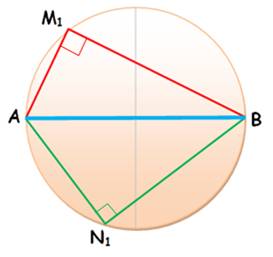
AB est un diamètre A M1 B = A N1 B A M1 B + A N1 B = 2 x A M1 B = A M1 B = /2 Les angles qui interceptent un diamètre sont des angles droits. (M étant bien entendu sur le cercle).	Les angles qui interceptent un diamètre sont droits.
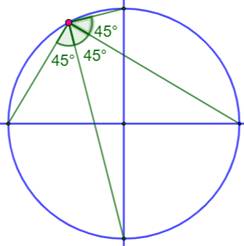
Avec deux diamètres orthogonaux Angles au centre: 90°. Angles inscrits: 45°

Voir Applications au calcul des angles de l'octogone /

Avec les tangentes: théorème des angles alternés

Démonstrations

Angle au centre et angle inscrit
Théorème Un angle au centre interceptant un arc AB vaut le double de l'angle inscrit interceptant le même arc AB. Anglais The angle at the centre of a circle is double of an angle at the circumference standing on the same arc.
Hypothèses Un cercle de centre O La corde AB. Un angle au centre AOB. Un angle inscrit AMB. Observations Les rayons sont égaux: R = OA = OB = OM Théorème invoqué La somme des angles dans un triangle est égale à = 180°. Conséquence Si AB est un diamètre: = 180° = 180° / 2 = 90° Un angle inscrit qui intercepte un diamètre est droit	Démonstration Le triangle MOA, avec OM = OA est isocèle. Ses angles à la base sont égaux OMA = OAM = a De même pour les deux autres triangles isocèles MOB et AOB avec les angles b et c. Dans le triangle AOB, la somme des angles vaut 180°: + 2c = = – 2c Dans le triangle AMB, la somme des angles vaut 180°: 2a + 2b + 2c = 2(a + b) = – 2c 2 = – 2c Rapprochons les deux égalités: = – 2c = 2

Voir Brève 51-1018

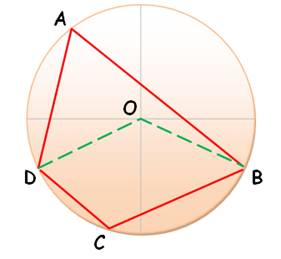
Une application aux quadrilatères L'angle en A vaut la moitié de l'angle en O. A = DAB = ½ DOB côté A L'angle en C vaut la moitié de l'angle en O. B = DCB = ½ DOB côtéC La somme de ces angles donne: A + C = ½ totalité de l'angle en O = ½ de 360° = 180°

Dans tout quadrilatère inscrit dans un cercle, la somme des angles en A et C, comme celle des angles en B et D vaut 180°.

Voir Jolie application au sujet de triangles équilatéraux

Polygones réguliers
Dans un polygone régulier, les côtés sont égaux (de même longueur) Les arcs interceptés sont égaux également. Les angles au centre interceptant des arcs égaux, sont égaux Dans cet hexagone, il y a six angles au centre qui couvrent 360°. Chacun mesure 360/6 = 60°. Les triangles internes sont équilatéraux. tous les angles mesurent 60°. Un angle au sommet, comprenant deux angles de 60°, vaut 120°.

Le parallélogramme – Exercice d'application
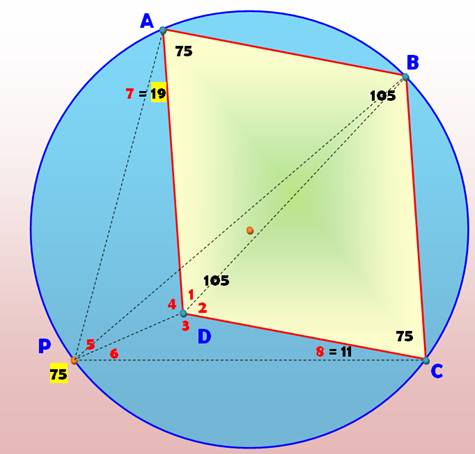
Un joli exercice de géométrie mettant en jeu les angles dans le cercle, les quadrilatères et les triangles. Un parallélogramme est tracé sur un cercle tel que sur la figure. Depuis un point P du cercle, la corde AC est vue sous un angle de 75°. L'angle PAD mesure alors 19°. Angles du parallélogramme, et valeur de l'angle PCD, noté 8?
Le quadrilatère ABCP est inscriptible, les angles opposés sont supplémentaires
Angles du parallélogramme: angles opposés égaux et supplémentaires à leurs voisins.
En D, tous les angles = 360°:
Avec les triangles latéraux: ADP et CDP:		255° + 19° + 75° + x = 360° x = 11°
Finalement, la valeur de l'angle 8:

Triangle dans le cercle et abscisses angulaires
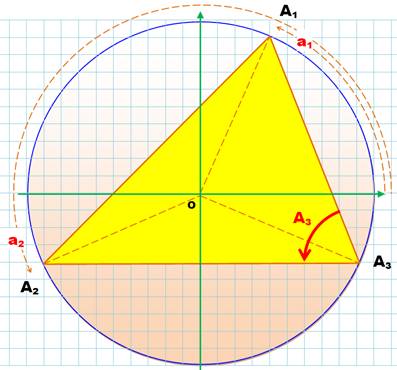
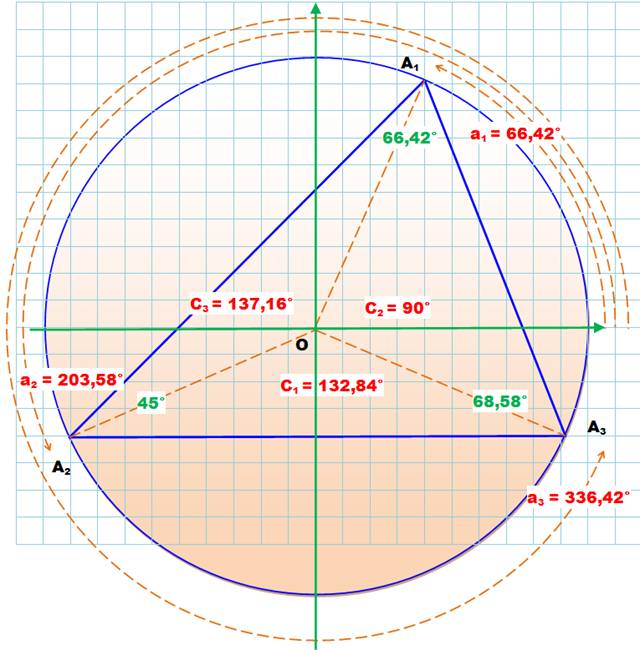
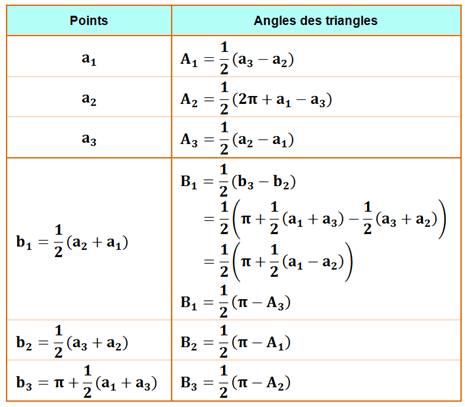
· Une brillante application (voir Auteur) de la propriété fondamentale des angles inscrits: L'angle au centre vaut deux fois l'angle inscrit interceptant le même arc. · Un triangle A1A2A3 inscrit dans un cercle. Les abscisses angulaires des sommets sont a1, a2 et a3 dans l'ordre croissant des valeurs.
Propriété Cet angle du triangle est égal à la demi-différence des abscisses angulaires des sommets des deux autres.
Pour les deux autres angles (précaution selon leur orientation). Illustration avec valeurs des angles Application numérique (pour s'exercer)

Angles du triangle conjugué
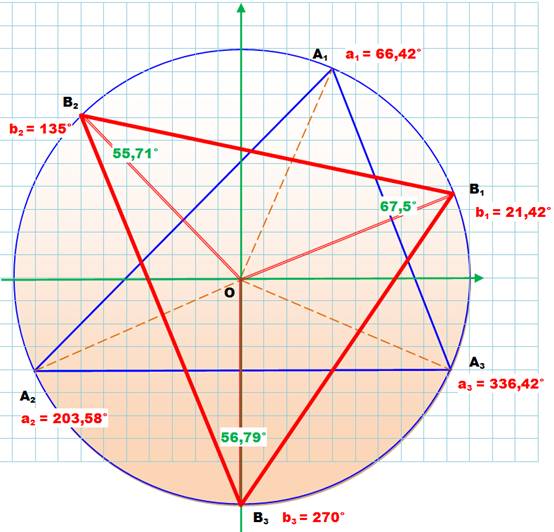
· On appelle triangle conjugué du triangle inscrit A1A2A3, le triangle B1B2B3 dont les sommets sont sur le cercle et sur les médiatrices des côtés du triangle originel. Dit-autrement, les nouveaux points sont situés au milieu des arcs initiaux. · Les abscisses angulaires de ces points milieu sont faciles à calculer: Illustration Calculs

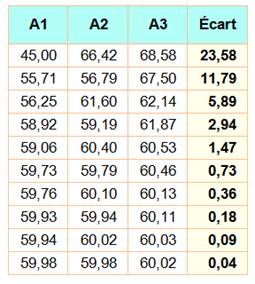
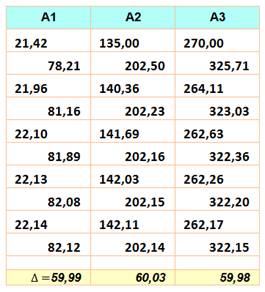
Convergence des triangles conjugués · Nous pourrions à nouveau calculer le conjugué du conjugué, etc. et démontrer que ces conjugués convergent vers un triangle équilatéral. La valeur des angles progressent vers les 60°. Le tableau montre la convergence des trois angles vers 60° après dix itérations. L'écart entre l'angle max et min (A3 – A1) est divisé par 2 à chaque itération. Voir Achille et la tortue
Démonstration de la convergence Le tableau donne les formules pour deux itérations. En prenant A1 < A2 < A3, nous constatons que les angles du triangle conjugué se retrouvent dans l'ordre suivant: B1 < B3 < B2. Soit un écart en max et min égal à: À chaque itération l'écart est divisé par 2.
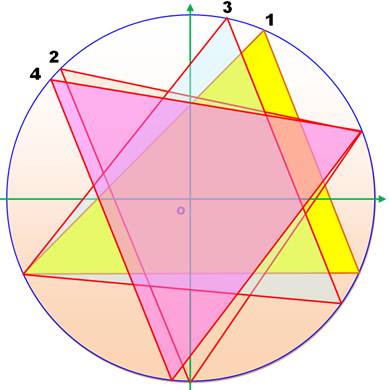
Position de convergence Si le triangle initial est équilatéral son conjugué est aussi équilatéral, et le suivant se superpose exactement au triangle initial (étoile à six branches). Un triangle isocèle conserve sa symétrie. Il reste isocèle tout en convergeant vers le triangle équilatéral. Un triangle isocèle extrêmement petit aura pour conjugué un triangle isocèle extrêmement effilé positionné sur un diamètre, les suivants vont vite se déployer pour converger vers un triangle équilatéral. Si le triangle de départ est quelconque, sa destinée est également équilatérale (cas de la figure et du tableau ci-contre). Les deux triangles équilatéraux de convergence sont orientés à 60° l'un de l'autre. Dans tous les cas, la figure finale de convergence est une étoile régulière à six branches. Les abscisses angulaires des sommets de ces triangles convergent avec un écart divisé par deux à chaque itération. Note: les valeurs numériques des abscisses restant dans la grande majorité des cas des nombres irrationnels.		Succession de triangles conjugués Les triangles conjugués successifs convergent en alternance vers deux triangles équilatéraux formant une étoile à six branches. Tableau des angles des triangles conjugués successifs pour dix itérations.

Auteur de cette propriété et de sa démonstration: Jean-Louis Breuil

Que je remercie grandement.

Suite	· Équations · Fondements
Voir	· Cercle – Index · Géométrie – Index
Cette page	http://villemin.gerard.free.fr/GeomLAV/Cercle/Angle.htm