|
||||||||||||||||||||||||||||||||||||||||
![]()
|
CERCLES INSCRITS Propriétés – Théorèmes |
|
ou théorème
de Thébault n°3 |
|
|
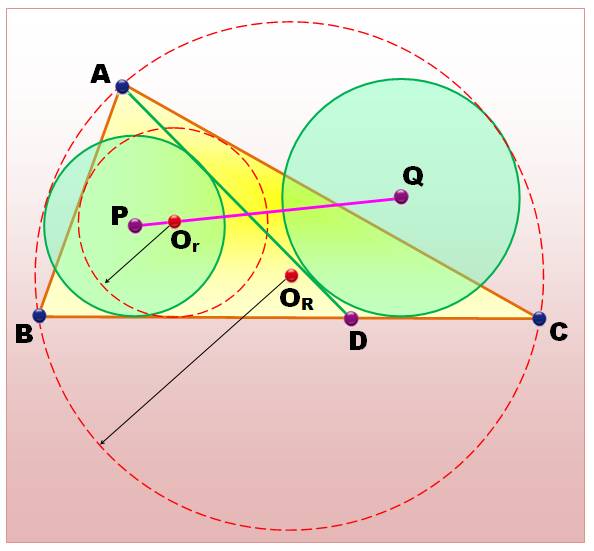
Données Un triangle quelconque ABC, et la
cévienne AD. Son
cercle inscrit de centre Or et circonscrit de centre OR. Les deux
cercles verts tangents aux droites BC et AD et
aussi au cercle circonscrit avec centre P et Q. Théorème Les centres P, Q
et Or sont alignés quelle
soit la position de D sur BC.
Historique En 1938, Victor Thébault (1882-1960), le mathématicien
français, a proposé un problème sur trois cercles de centres colinéaires de
ce type. En 1973, démonstration par mathématicien néerlandais H. Streefkerk. En 2003, Jean-Louis Ayme publie une nouvelle
solution et, en faisant des recherches historiques, découvre que le théorème
avait été démontré en 1905 par la japonais Y. Sawayama.
Dans les années 1970, le mathématicien chinois Wenjun
Wu (1919-2017) a élaboré une technique de résolution algébrique qui a permis
de démontrer automatiquement de nombreux théorèmes de géométrie déjà connus
dont celui-ci. Démonstration Voir les sites indiqués (démo pas
immédiate !) |
|
![]()
|
Suite |
|
|
Voir |
|
|
Site |
|
|
Cette page |
![]()