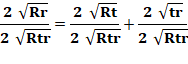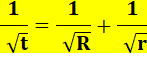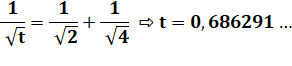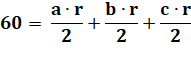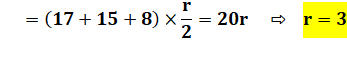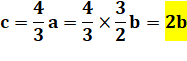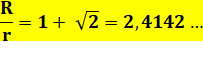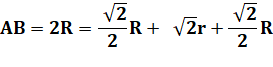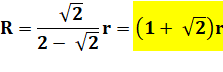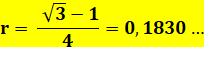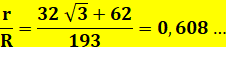NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 21/11/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	CERCLE
Débutants Géométrie	CERCLES INSCRITS …				Glossaire Géométrie
INDEX Défis en géométrie Cercles Triangles	Index	Inscrit	SANGAKUS	Deux cercles – Triangle
	Introduction	Inscrit (suite)	Jumeaux	Deux cercles – Carré
	Puissance	Circonscrit	Carré max	Deux cercles – Carré et triangle
		Exinscrits	Face à face	Trois cercles – Construction
	Chapelet de cercles			Trois cercles – Tr. Équilatéraux
				Quatre cercles – Construction
		Sommaire de cette page >>> Théorème japonais >>> Triangle rectangle Sangaku >>> Les trois cercles en tangence entre eux et au sol >>> Triangle rectangle et ses cercles inscrit / circonscrit >>> Triangle, carré et cercles >>> Les six cercles >>> Trois cercles et un triangle >>> Cinq cercles dans un carré >>> Sangaku de Takasaka – Éventail de la Geisha

SANGAKUS

Cercles et géométrie

Initialement les Sangakus sont des tablettes votives utilisées dans les temples japonais. On y trouve des énigmes géométriques qui sont devenues des exercices ou énigmes appréciées des amateurs de géométrie.

Sangaku veut dire tablettes mathématiques. Période: 1639 à 1854. On connait encore de l'ordre de 800 tablettes.

Trois centres d'intérêt:

L'esthétique de ces figures géométriques;

La formulation des proportions entres les objets; et

La méthode de construction de ces dessins (Voir Jumeaux d'Archimède).

Théorème japonais		haut
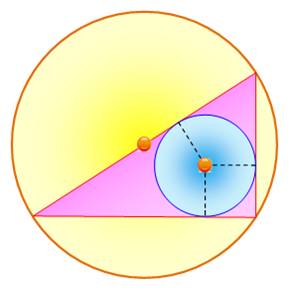
Sangaku Vieux théorème japonais cité par Roger Johnson Advanced Euclidean Geometry (1929) Soit un polygone convexe à n côtés inscrit dans un cercle. On choisit une triangulation du polygone et on trace les cercles inscrits dans les triangles. La somme des rayons des cercles inscrits est alors indépendante de la triangulation choisie. Source image : Tangente n°24 – Le Triangle
Exemple

Triangle rectangle Sangaku
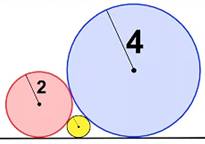
Triangle somme et différence Un triangle rectangle dont l'hypoténuse est égale à la somme de deux longueurs (R et r), alors qu'un des côtés vaut la différence des longueurs. Alors, le troisième côté vaut deux fois la moyenne géométrique des longueurs R et r. Vu autrement: deux cercles adjacents sur un sol plat; le carré de la distance au sol (AB) est égal à quatre fois le produit des rayons des cercles.
Théorème de Pythagore	AB² = (R + r)² – (R – r)² = R² + 2Rr + r² – R² + 2Rr – r² = 4Rr

Voir Autres triangles rectangles

Les trois cercles en tangence entre eux et au sol
Application des résultats précédents: AB = AC + CB	Voir Construction géométrique
La réponse à cette énigme Internet est donc:

Voir Moyenne harmonique

Merci à Marc H. pour sa contribution

Triangle rectangle et ses cercles inscrit / circonscrit
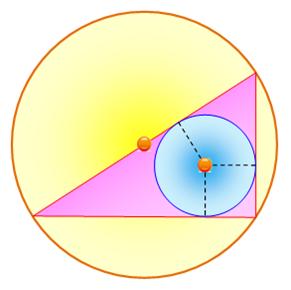
Triangle rectangle b = 15 et c = 8. L'hypoténuse vaut alors: a² = 15² + 8² = 289 et a = 17. L'hypoténuse est un diamètre du cercle circonscrit au triangle rectangle et vaut donc 17. Pour calculer le rayon du cercle inscrit, on va utiliser l'aire du triangle rectangle: A = 15 x 8 = 60. Les trois hauteurs découpent trois triangles dont les aires sont:

Triangle, carré et cercles

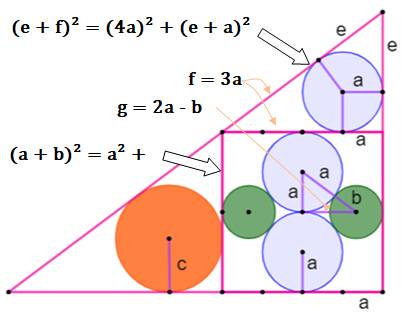
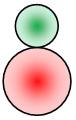
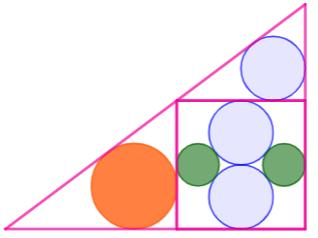
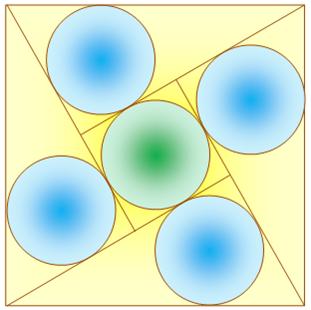
Problème

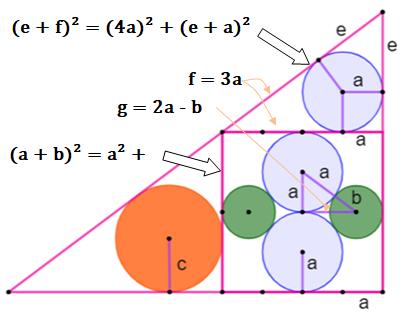
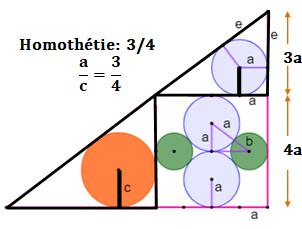
Sur cette figure, montrer que le rayon du cercle orange est le double de celui du cercle vert.

Solution

Essentiellement le théorème de Pythagore dans les triangles rectangles, et Théorème de Thalès pour un rapport d'homothétie.

Triangle du haut	(e + f)² = (e + 3a)² = e² + 6ae + 9a² = 4ae e =	(4a)² + (e + a)² 16a² + (e + a)² 16 a² + e² + 2ae + a² 8a² 2a
Son côté à droite	a + e = 3a
Triangle interne	(a + b)² = a² + 2ab + b² = 6ab = 3b =	a² + (2a – b)² a² + 4a² – 4ab + b² 4a² 2a
Homothétie

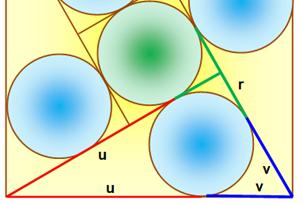
Figures et notations

Les six cercles
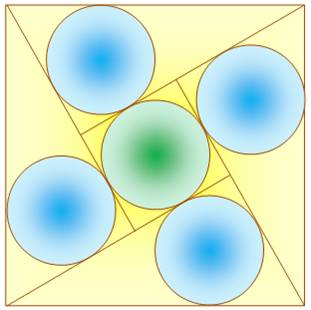
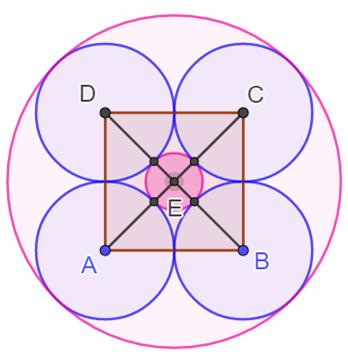
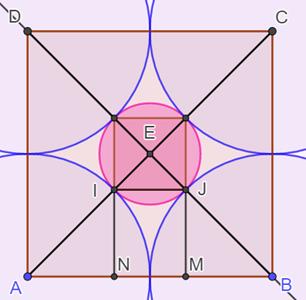
Problème Quatre cercles tangents deux à deux et chacun tangent à un grand cercle. Quel est le rapport entre le rayon des cercles internes, grand sur petit ? Solution Les centres des quatre cercles forment un carré. Les diagonales se croisent à angle droit. Le triangle AEB est droit en E. Théorème de Pythagore AB² = AE² + BE² (2R)² = (R + r)² + (R + r)² 4R² = 2R² + 4Rr + 2r² R² – 2Rr – r² = 0 Équation du deuxième degré Choix de la valeur positive:	Si r = 1 alors R = 2,4142… AB = 2R = 4,8284… AC = 2R + 2 = 6,8284… Diamètre = AC + 2R = 11,6568…
Calcul direct (sans équation) AB = 2R = AN + NM + MB Dans IEJ: IJ² = 2r² Dans AIN: R² = AN² + NI² = 2 AN² En remplaçant dans AB

Trois cercles et un triangle
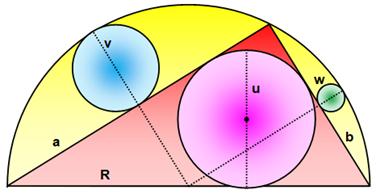
Problème Un triangle rectangle (2a, 2b, 2R) inscrit dans un demi-cercle de rayon R. Deux petits cercles (r et r') inscrits dans les segments de cercle. Relations entre les trois diamètres ? Solution
Relations liées au rayon du grand cercle	R = b + 2v = a + 2w
Rayon du cercle inscrit (Attention aux notations en moitié de côté)	2u = 2a + 2b – 2R u = a + b – R u = R – 2w + R – 2v – R u = R – 2(v + w) R = u + 2(v + w)
Retour aux côtés du triangle	b = R – 2v = u + 2(v + w) – 2v = u + 2w a = R – 2w = u + 2(v + w) – 2w = u + 2v
Théorème de Pythagore	(2R)² = (2a)² + (2b)² R² – a² + b² = 0 (u + 2(v + w))² = (u + 2v)² + (u + 2w)²
Développement effectué	u² = 8 v.w

Cinq cercles dans un carré
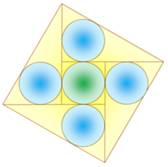
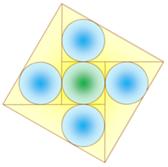
Un carré est découpé en quatre triangles rectangles et un carré central. Les cercles inscrits sont tous identiques. Quel est leur rayon rapporté au côté du carré ? Dans le triangle rectangle du bas, les distances aux points de tangences sont égales: (u = u; v = v et r = r) Théorème de Pythagore: (u + v)² = (u + r)² + (v + r)² Côté du carré: c = u + v Grand côté oblique du triangle rectangle: u = v + 2r Leur somme: c + u = u + v + v + 2r => v = c/2 – r Leur différence: c – u = u + v – v – 2r => u = c/2 + r En reprenant la somme des carrés: c² = (c/2 + r + r)² + (c/2 – r + r)² => 8r² + 4cr – c² = 0 Racine positive:	Le côté du carré c = 5,46 r Côté du triangle rectangle: 0,5 c et 0,8666… c Angles 30° et 60° C'est un triangle rectangle 30, 60

Anglais: Five incircles in a square

Sangaku de Takasaka – Éventail de la Geisha
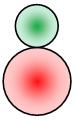
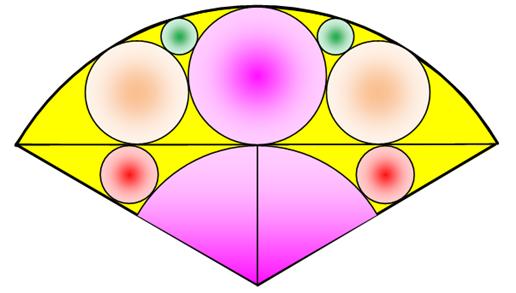
Ce Sangaku est présenté par Pickover dans son livre. Il est dû au jeune (11 ans) Kinjiro Takasaka (1873). Rapport entre les diamètres de deux petits cercles: le rouge (en bas) et le vert (en haut):

Voir Le calcul de la formule par Géry Huvent

Suite	Arbelos Carré et deux cercles tangents Chaine de Pappus Défis en géométrie Rayon du cercle circonscrit Cercle inscrit Puissance d'un point par rapport à un cercle
Voir	Bissectrices Cercle – Index Cercles et triangles Cône Diamètre Géométrie – Vocabulaire Périmètre Sphère
DicoNombre	Nombre 0,5858…
Livres	Quand les Sangakus s'invitent à la table – Tangente n°158 – Mai et juin 2014 Sangaku, le mystère des énigmes géométriques japonaises – Géry Huvent – Dunod Mysteries of the equilateral triangle – Brian J. McCartin – Figure 4.32 The Maths Book – Clifford A. Pickover – Sangaku Geometry – Page 198 Modern Sangaku – Jean Constant – Hermay NM – 2018 - Sangakus artistiques
Sites	Sangaku – Wikipédia Wasan – Gery Huvent – 2009 – Nombreux exemples de Sangakus L'éventail de la Geisha – Géry Huvent – 2009 Sugaku – Géry Huvent Olympiades académiques 2008 – Descartes et les Mathématiques 11) Sangakus : 2 cercles tangents dans un carré – Mathieu Morinière Sangaku – Cut The Knot – Réflexions et Index d'accès à de nombreux Sangakus Sangaku Journal of Mathematics – Quantité d'exemples de Sangakus
Cette page	http://villemin.gerard.free.fr/GeomLAV/Cercle/Sangakus.htm