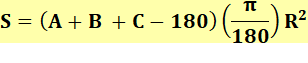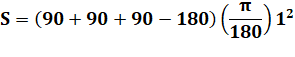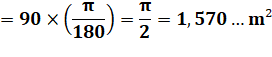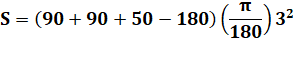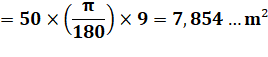|
|||||||||||||||||||||||||||||
![]()
|
Les trois GÉOMÉTRIES Depuis que l'on ne s'interdit
plus de penser que des parallèles (Postulat d'Euclide) ne se
coupent pas même à l'infini, on parle de
géométries au pluriel. La géométrie
est l'une des branches les plus anciennes des mathématiques. D'abord
euclidienne, elle va s'ouvrir à deux cousines. |
Cinquième postulat d'Euclide

Voir Droites
parallèles
Huit géométries en dimension 3
|
Dans les années 1970 et 1980, l'Américain William Thurston (1946-2012) s'est rendu
compte que de nombreux espaces topologiques
de dimension 3 sont géométrisables. De même qu'en dimension 2, la géométrie euclidienne a
deux "sœurs", la géométrie sphérique et la géométrie hyperbolique,
en dimension 3 la géométrie euclidienne est aussi membre d'une fratrie plus
nombreuse. Outre les géométries sphérique et hyperbolique (analogues à celles
de la dimension 2), on compte cinq autres géométries, les géométries
de Thurston. |
Étienne Ghys – CNRS
et École Normale Supérieure de Lyon
|
|
||
|
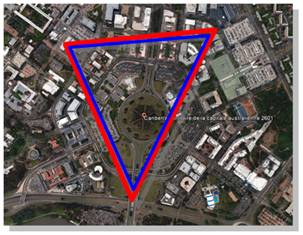
Canberra, capitale de l'Australie Dessiner un triangle reliant trois points de la capitale est un exercice classique. La
surface peut être considérée comme plate. La somme des angles de ce
triangle, posé sur un plan, est égale à 180°. C'est la géométrie classique
dite euclidienne. |
|
|
|
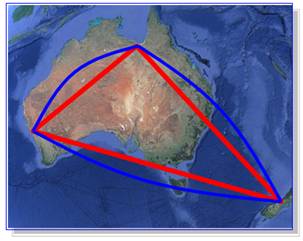
Australie et Nouvelle Zélande Dessiner un
triangle reliant trois points sur la sphère
terrestre est faisable dans l'absolu (rouge). Cependant, le parcourir en
réalité, il faut suivre la courbure terrestre (bleue). La somme des
angles est alors plus grande que 180°. C'est la géométrie sphérique. |
|
|
|
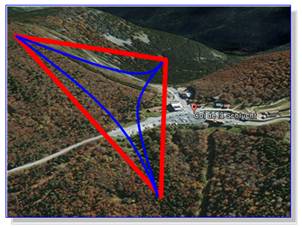
Le col de la Schlucht dans les Vosges Dessiner un
triangle reliant trois points (rouge) pourtant proche est toujours possible par
la pensée. Cependant, en suivant le terrain, on forme un tout autre triangle
(bleu). C'est la géométrie hyperbolique,
dite aussi en selle de cheval; image qui concorde bien avec celle d'un col en
montagne. |
|
|
Voir Géographie
|
|
|||
|
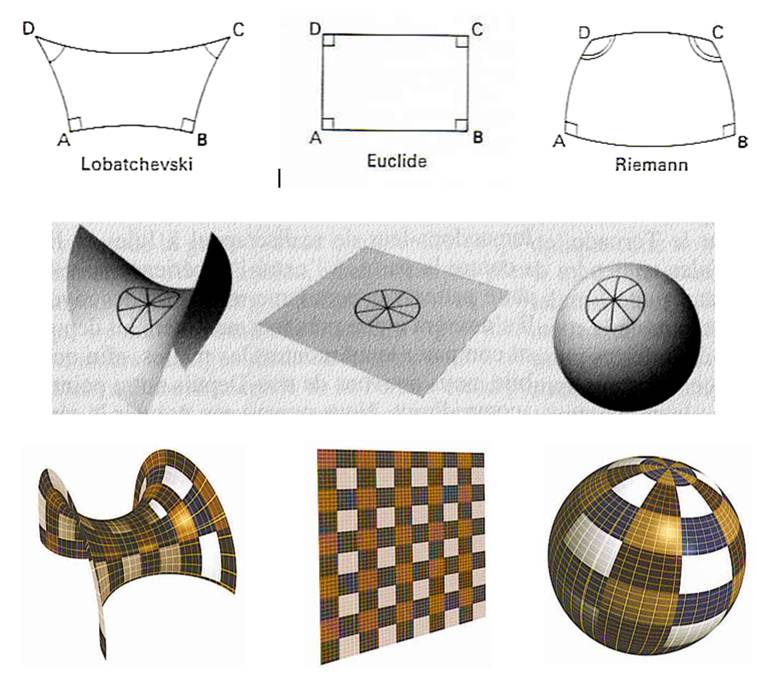
Selon la courbure |
|||
|
NÉGATIVE Hyperbolique (selle de
cheval) Lobatchevsky
(1826) |
NULLE Euclidienne Voir Euclide
(vers -330) |
POSITIVE Élliptique ou Sphérique Riemann (1854) Voir Triangle sphérique |
|
|
Huperbolic geometry Saddle geometry Lobatchevskian
geometry |
Euclidean geometry |
Riemannian geometry Elliptic geometry Spherical geometry |
|
|
Angle
aigu (triangle: < 180°) |
Angle
droit (triangle: 180°) |
Angle
obtus (triangle: >180°) |
|
|
Sphère |
Plan
euclidien |
Pseudo-sphère |
|
|
2
(ou infinité) |
1
parallèle |
0
parallèle |
|
|
|
|
|
|
|
|
|
|
|
|
En trois dimensions |
|||
|
Infinité
de formes. Surfaces à
trous ou à anses. Esher a tenté toute sa vie de
représenter de telles formes. Il existe
une infinité de sortes d'espaces à courbure négative: certaines
fermées (finies), d'autres
ouvertes (infinies). |
Cinq
formes génériques: Plan, Cylindre, Tore Ruban de Moebius Il existe
18 sortes d'espaces tridimensionnels à courbure nulle, de topologies
distinctes: espace
euclidien ordinaire, supertore,
etc. |
Deux
formes: Sphère et
plan projectif (difficile
à représenter). |
|
|
Modèle de l'Univers de
Fiedmann-Lemaître selon la courbure de l'espace. |
|||
|
Espace
ordinaire hyperbolique infini |
Espace
euclidien ordinaire infini |
Sphère à
trois dimensions, finie pour l'espace sphérique. |
|
Voir Courbure
Illustrations du bas:
À l'image des GÉANTS – Stephen Hawking – Préface Jean-Pierre Luminet – Dunod -
2005
|
Pour
prouver le 5e postulat, Saccheri (1667-1733) et Legendre
(1752-1833) font l'hypothèse qu'il est faux et tente de trouver une
contradiction. Saccheri commettra une erreur et Legendre croit y arriver,
mais il a introduit un nouvel axiome: une droite passant par un point
intérieur à un angle coupe les droites portées par les côtés de l'angle.
Évident, mais pas démontré. |
|
|
||
|
Euclide (vers -300) |
Postule que les parallèles
ne se rencontrent jamsi (sous une autre
formulation). |
|
|
Posidonius (vers – 100) |
Les droites parallèles sont des
droites coplanaires équidistantes: leurs perpendiculaires créent des segments
égaux. |
|
|
Géminus (vers – 100) |
Attire l'attention sur le
phénomène asymptotique de l'hyperbole.
Pourquoi n'existerait-il pas pour les droites parallèles? |
|
|
Proclus (412-485) |
Il démontre que si une
droite coupe une droite, elle coupe aussi ses parallèles. En fait, il suppose
le postulat sans s'en apercevoir. Idée pour la démonstration: la distance
entre deux droites parallèles est une quantité finie. |
|
|
Mathématiciens arabes |
Ils sont au moins cinq à
avoir tenté la démonstration du postulat. |
|
John Wallis (1616-1703) |
Fait admettre l'existence des
figures semblables et de leur proportionnalité. Laplace pense que cette
assertion est plus naturelle que celle d'Euclide. |
|
Girolamo Saccheri (1667-1733) |
Montre que la similitude revient
à dire que pour tout triangle, il en existe d'autres de mêmes angles. Il énonce les bases de la
géométrie non-euclidienne, sans y croire vraiment car trop absurde. Idée pour la démonstration: un quadrilatère
ayant deux côtés égaux et perpendiculaires aux deux autres est un rectangle. |
|
Johann Lambert (1728-1777) |
Theorie der Parallellinien
(1786) Reprend une idée qui date
des mathématiciens arables (Ibn al-Haytam) du quadrilatère à trois angles
droits et spécule sur la valeur du quatrième: droit, aigu ou obtus. Idée pour la démonstration: Un quadrilatère
ayant trois angles droits est un rectangle. |
|
Adrien Marie Legendre (1752-1833) |
Dans Éléments de géométrie
(1794 à 1823) tente la démonstration, mais au prix de l'introduction d'une nouvelle
hypothèse équivalente au postulat. |
|
Trois
mathématiciens vont introduire quasi-simultanément les nouvelles géométries:
Gauss, Bolyai et Lobatchecsky |
|
Carl Gauss (1777-1855) |
Les travaux de ces
précurseurs, comme le craignait Gauss,
n'ont pas entraîné l'enthousiasme. Il se serait attelé au
cinquième postulat dès ses 15 ans. Il
montre qu'il revient à démontrer qu'il existe un triangle d'aire aussi grande
que l'on veut. Il découvre une nouvelle géométrie vers 1813 mais n'ose pas la
publier car trop indigeste pour ses amis, pens-t-il. |
|
Janos Bolyai (1802-1860) |
Militaire à la retraite à 31
ans, mathématicien hongrois. Fils d'un mathématicien amis
de Gauss qui avait pour passion le fait
de démontrer le cinquième postulat. En 1820, il abandonne la
démonstration et décide de développer une géométrie sans l'axiome des
parallèles (La science absolue de l'espace – 1829). Gauss prend connaissance de
ces travaux et l'informe qu'il connaissait ces résultats depuis trente ans,
mais ne les avait pas publiés de peur des réactions de ses pairs. |
|
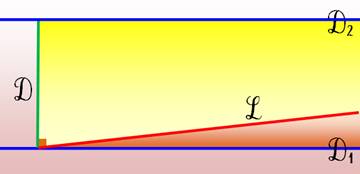
Nikolai
Lobatchevsky (1792-1856) |
Mathématicien russe, recteur
de l'université de Kazan. Géométrie imaginaire publié
en russe en 1829, puis en français en 1837. Elle dit que par un point
extérieur à une droite passent deux droites parallèles à cette droite. Argument de Lobatchevsky Soit deux droites D1 et D2. La perpendiculaire D à D2 coupe D2. La perpendiculaire D1 à D ne coupe pas D2. Il existe ainsi des droites qui coupent D2 et d'autres qui
ne la coupe pas.
Si L est la droite limite entre ces deux classes de droites, les
droites dans la région jaune coupent D2 et celles de la région
ocre ne la coupe pas. La suite va s'appliquer à la valeur de l'angle entre L et D1 (angle
de parallélisme). Lobatchevsky va en faire une fonction de la longueur de D. Pour lui, si cette longueur croit de 0 à l'infini, l'angle décroît de
Pi/2 à 0. Formule de l'aire du
triangle en fonction des angles. |
|
Beltrami,
Klein, Poincaré, Hilbert, Riemann |
Mathématiciens ayant
contribué à développer les géométries non-euclidiennes. |
|
Bernhard
Riemann (1826-1866) |
Il
révolutionne les concepts (1854):
|
Le cercle de Poincaré et celui tel que vu par Esher et celui
|
Cercles
symbolisant l'horocycle de Lobatchevsky: ligne courbe dans un plan telle que
toutes les médiatrices de ses cordes soient parallèles entre elles. |
Voir Cercle de Poincaré / Cercle
|
|
||
|
|
Exemple 1 A = B = C = 90° et
R = 1 m
Exemple 2 A = B = 90° C = 50° et R =
3 m
|
|
![]()
|
Suite |
|
|
Incontournables |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Geometri/GeoTrois.htm
|
![]()