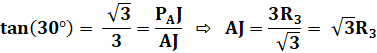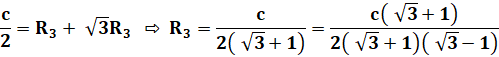NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 30/11/2024 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	TRIANGLES
Débutants Triangle	Propriétés – Curiosités				Glossaire Triangle
INDEX Types de triangles Triangle	Point Milieu	Droites et points	Pappus	Point et triangles
	Angles (180°)	Quantité de triangles	Torricelli	Triangles et triangles
	Médianes	Quatre triangles	Heilbron	Carrés triangles
		Représentation	Brocard	Cercles et triangles
	Cercles et triangle équilatéral			Demi-cercle et triangle
		Sommaire de cette page >>> Triangle équilatéral inscrit dans un cercle >>> Bilan >>> Cercles inscrits >>> Les trois cercles inscrits

Voir Propriétés fondamentales des triangles

TRIANGLE ÉQUILATÉRAL & CERCLES

D'abord le simple triangle équilatéral inscrit dans le cercle, puis …

Fameux théorèmes donnant la relation entre les angles inscrits et les angles au centre interceptant le même arc.

Quels sont les cercles internes associés au triangle équilatéral?

Triangle équilatéral inscrit dans un cercle		haut
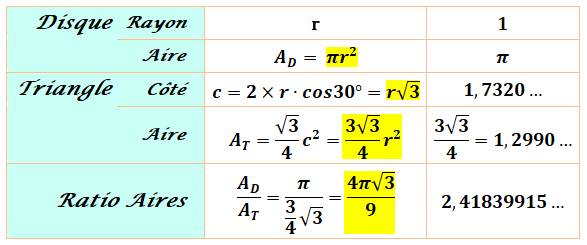
Construction Un cercle de rayon unité (r = 1). Construction classique de la rosace. On dispose alors de six points également repartis sur la circonférence. En choisissant un point sur deux, on construit le triangle équilatéral. But Calculer la longueur du côté du triangle équilatéral, son aire et le ratio entre les deux surfaces disque et triangle équilatéral.	Pour un cercle unité, la longueur du côté du triangle équilatéral inscrit est racine de 3.
Calculs

Voir Suite et détails / Brève 50-997 / Cercle inscrit dans le triangle équilatéral

Bilan – Récapitulatif des formules (explications ci-dessous)
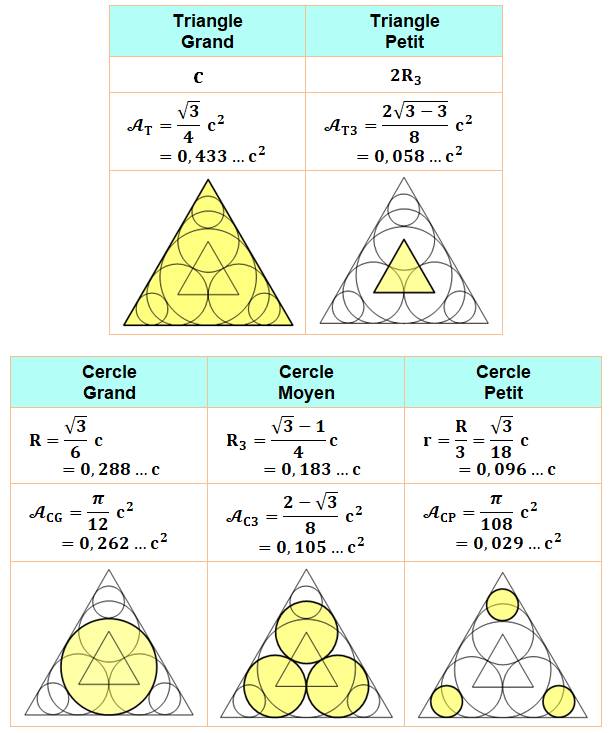
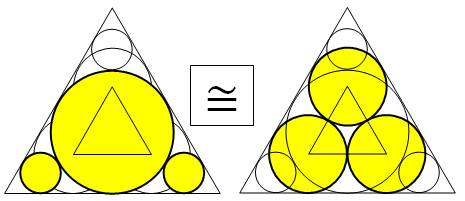
Un triangle équilatéral de côté c La première ligne du tableau donne les formules des longueurs. La deuxième, les aires des surfaces en jaune (un seul disque sur les deux dernières figures) La troisième ligne montre une miniature des figures. Comparaisons 1CG + 2CP 3CM Écart: 0,0043 (1,3 %) 2CP 1TP Écart: 0,00016 (0,3 %) 1GT 1CG + 1CM + 3CP Écart: 0,021 (4,9 %)	Comparaison

Détails des calculs

Cercles inscrits
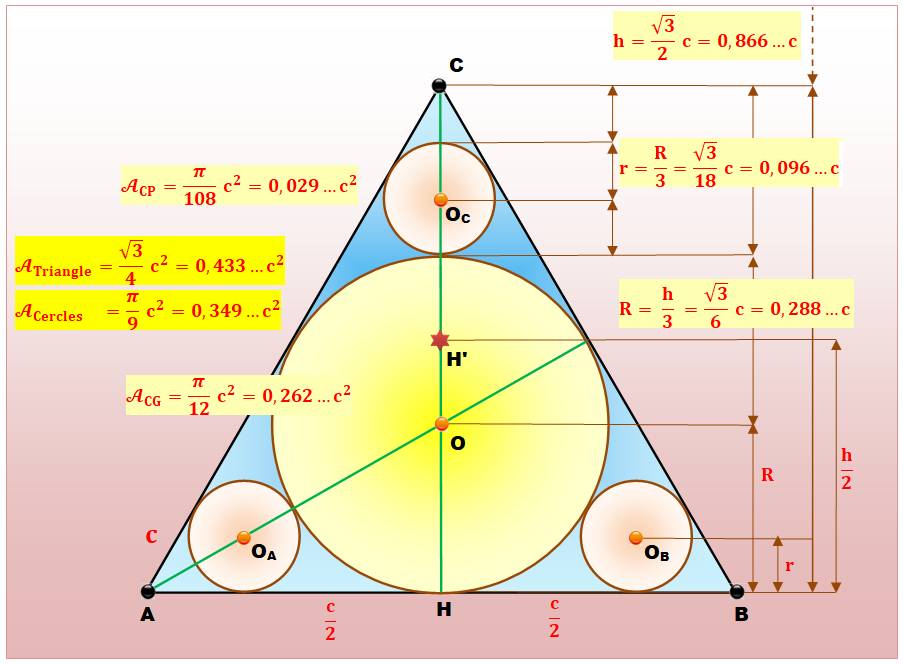
Un triangle équilatéral et son cercle inscrit. Trois petits cercles inscrits dans les angles aux sommets.	Rayons et aires de ces cercles.

Les trois cercles inscrits
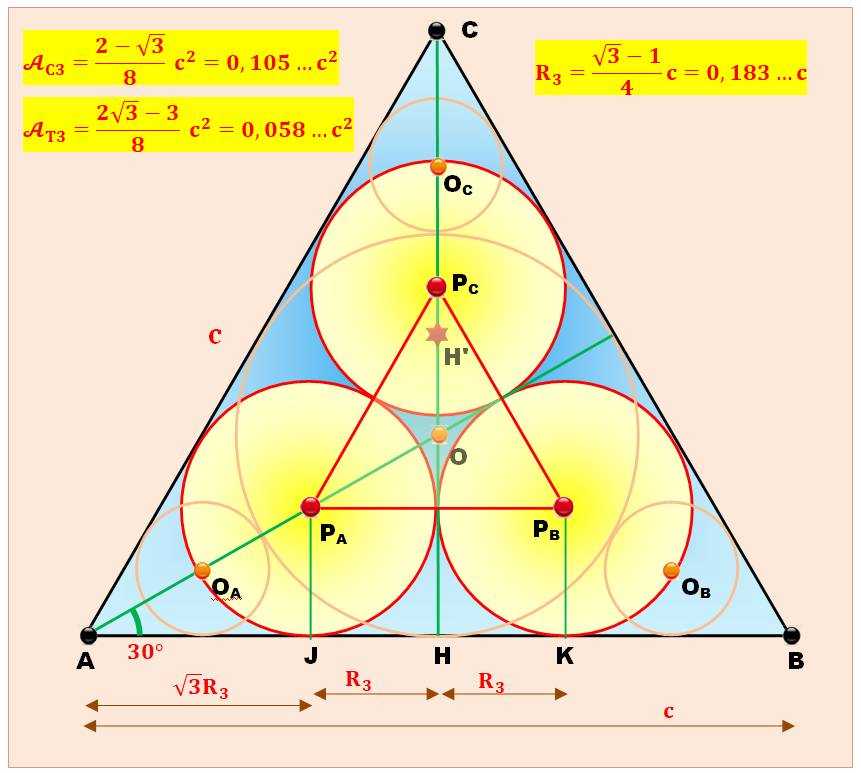
Le même triangle équilatéral et trois cercles inscrits. On a laissé la trace des cercles précédents. Notez que les centres des petits cercles ne sont pas sur la circonférence des nouveaux cercles.		Rayons et aires de chacun de ces cercles.
Calcul de AJ
Calcul de R3

Suite	Cercle inscrit dans le triangle équilatéral Cercles et triangles Triangles et carrés Cordes et triangles équilatéraux Cercle inscrit dans le triangle équilatéral Angles dans le cercle
Voir	Triangle – Index Cercle DicoMot Losange et son cercle inscrit Points caractéristiques du triangle
Cette page	http://villemin.gerard.free.fr/GeomLAV/Triangle/Propriet/TrgEqCer.htm