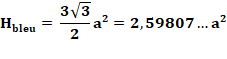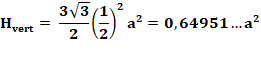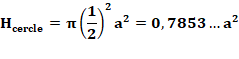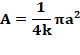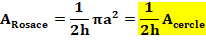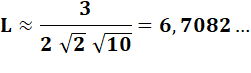|
||||||||||||
![]()
|
Rosaces Rhodonea / Rose Amusement, décoration, vitraux …
mais aussi en mathématiques:
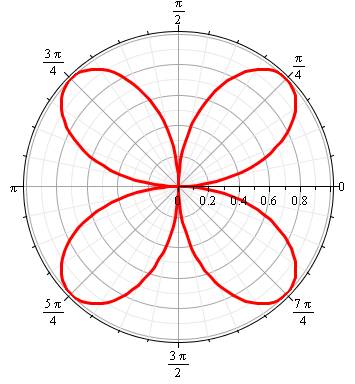
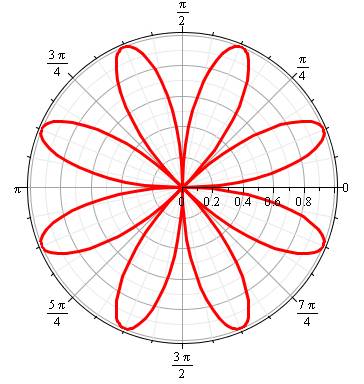
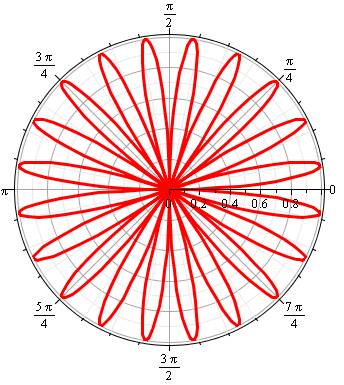
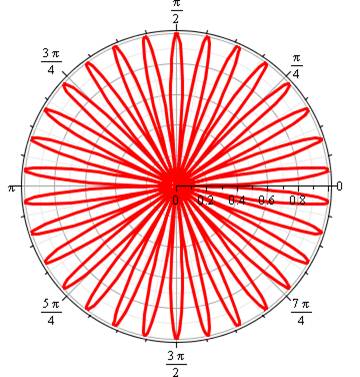
Famille de courbes du type R = sinus
(k.T) en coordonnées polaires, avec k un nombre rationnel supérieur à 1.
C'est le mathématicien italien Guido
Grandi (1671-1742) qui a Rosette est un nom réservé aux rosaces dont
les pétales se chevauchent. |
Anglais: k-petal rose / A curve which has the shape of a
petalled flower / Rhodonea / Rose-rhodonea curve
Grec: rhodo = rose
|
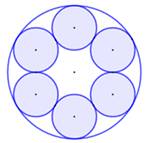
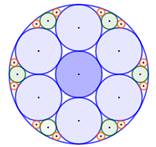
Construction Un hexagone
et des demi-cercles construits sur les côtés. Observation Le premier dessin montre une figure rose à
pétales. En repliant les pétales, on obtient la figure du
bas. Conclusion Aire rose est égale = aire verte Hexagone interne Aire de l'hexagone bleu = 4 × aire de
l'hexagone vert (côtés moitiés). Aires
|
|
|
Voir Brève 63-1258
|
|
|
|
Aire de cette rosace:
Voir Calcul |
|
Voir Construction hexagone / Six cercles +1
|
Voici une frise faite avec ce motif de rosace à six pétales
|
|
Un
exemple de rosace à 10 pétales
|
Voir Décagone
|
ou autres édifices religieux |
|
||
|
6 pétales - octogone
|
|
||
|
8 pétales - octogone
|
|
||
|
Voir Décagone |
|
||
|
12 pétales - dodécagone
Voir Dodécagone |
|
||
|
16 pétales - hexadécagone
|
|
||
|
|
|
|
|
|
![]()
|
|
||||
|
Équation Quantité de pétales Aire d'un pétale Aire des pétales |
Q = h. k
|
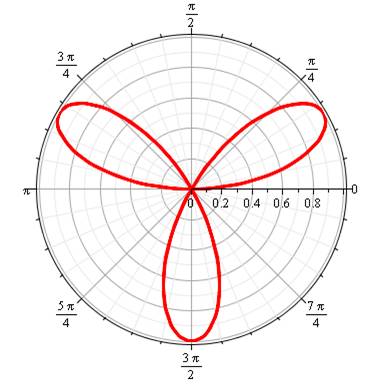
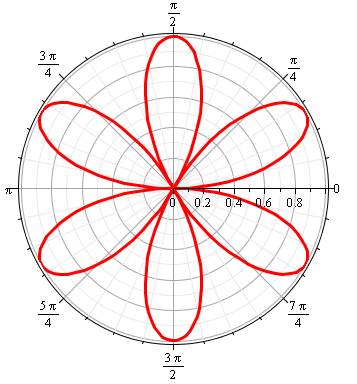
k pair => 2k pétales: h = 1 k impair => k pétales: h = 2 k impair avec calcul en valeur absolue => 2k pétales: h = 1 |
||
|
Aires par rapport au cercle |
Aire dans pétales = Aire
hors pétale pour n pair Aire dans pétales = ½ Aire hors pétale pour n impair |
|||
|
|
|
|||
|
|
|
|||
|
|
|
|||
Anglais: In
mathematics, a rose or rhodonea curve is a sinusoid plotted in polar coordinates.
![]()
|
Suite |
|
|
Retour |
|
|
Voir |
|
|
Diconombre |
|
|
Site |
|
|
Cette page |
![]()