![]()
|
|
Ce site est désormais accessible en |
|
22 Novembre 2025
![]()
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
Nombres CARRÉS INDEX (portail) |
Angl
Le saviez-vous?
|
2 x 3 + 3 = 3² 3 x 4 + 4 = 4² 4 x 5 + 5 = 5² 99 x 100 + 100 = 100²
Aucun mystère: (n – 1)
n + n = n² – n + n = n² |
ZENZIC of 2 = 2² = 4 ZENZICZENZIC of 2 = 24 = 16 ZENZICZENZICZENZIC of 2 = 28 = 256 Curiosité obsolète en
vieil anglais. Connu pour la quantité
de Z. |
Reconnaitre un carré d'un coup d'œil
|
L'unité
d'un carré n'est jamais 2, 3, 7 ou 8. Les
carrés se terminent par ces deux derniers chiffres uniquement. |
|
|
|
||||||||||||||||||||||||
|
Nombres carrés – Généralités |
|
|||||||||||||||||||||||
|
Place |
|
|||||||||||||||||||||||
|
Famille |
|
|||||||||||||||||||||||
|
||||||||||||||||||||||||
|
Racine |
|
|||||||||||||||||||||||
![]()
|
Usage |
|
|
>>> Carrés
des nombres de 1 à 199 >>> Carrés des nombres
de 1 à 99 selon leurs deux derniers chiffres >>> Carrés et cubes des
repdigits >>> Carrés et cubes sommes
d'impairs >>> Carrés, cubes et
jusqu'à puissance 9 des nombres de 1 à 25 >>> Différences de
carrés pour les nombres de 1 à 100 >>> Différences
de carrés – Tableau 15 x 15 >>> Nombres de 1 à 100 et leurs
sommes de carrés >>> Nombres de
Brahmagupta-Fibonacci (somme de deux carrés) >>> Nombres, sommes de 2,
3 et 4 carrés >>> Partition
en carrés de quelques nombres >>> Somme des carrés, cubes et jusqu'à puissance 9 >>> Sommes des carrés de n nombres successifs >>> Sommes des carrés, cubes jusqu'à puissance 7 >>> Triplets de Pythagore |
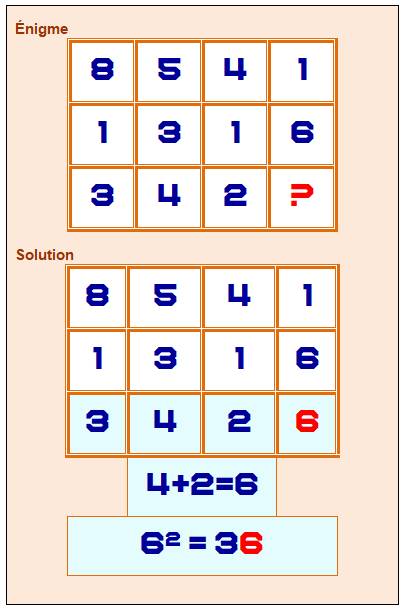
Problème mettant en jeu les carrés des nombres
Énigme 8541 – Trouver la
valeur manquante dans la grille.
Voir Énigmes virales
|
|
|
|
|
|
![]()
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()