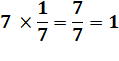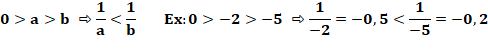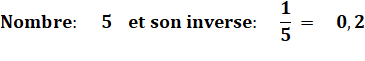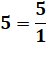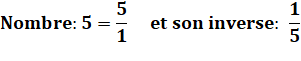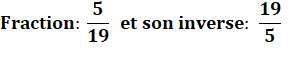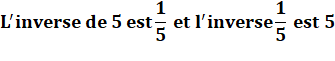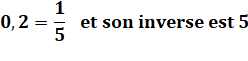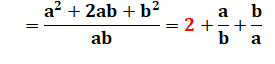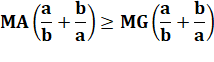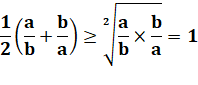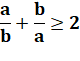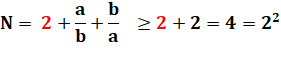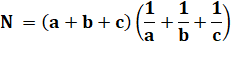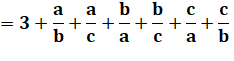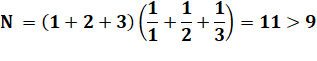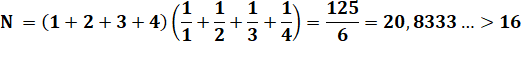Orientation Glossaire	Atlas / Nombres / Division Fraction / Règle de trois / Pourcentage
Débutant DicoMot DicoNombre	INVERSE d'un nombre, d'une fraction
Sommaire	>>> Approche et définition >>> Propriétés des inverses >>> Inverses des relatifs, fractions, décimaux >>> Inverse sur calculatrice >>> Somme des inverses et carrés >>> Énigme >>> Anglais

Approche
Définition	L'inverse d'un nombre est tel que le produit du nombre et de son inverse est égal à 1.

Voir Exemple de construction

Propriétés	Tout nombre n possède un inverse: 1/n, sauf le nombre 0, car 1/0 n'est pas défini. Le nombre 1 est son propre inverse. On note: Élever un nombre à la puissance -1 consiste à prendre son inverse. Rangement: l'inverse "inverse" le sens:
Écriture décimale Allure de la décroissance

Nombres relatifs	Un nombre realtif conserve son signe lorqu'on prend son inverse: Ne pas confondre avec l'opposé d'un nombre qui est ce nombre avec un signe opposé (Ex: l'opposé de 5 est -5).
Fractions	Tout nombre entier s'écrit sous la forme d'une fraction dont le dénominateur est l'unité: Prendre son inverse consiste à inverser numérateur et dénominateur (on dit aussi permuter numérateur et dénominateur): L'inverse d'une fraction consiste à inverser le numérateur (nombre en haut) et le dénominateur (nombre en bas). Donc, échanger le nombre du haut par celui du bas: L'inverse d'une fraction relative peut avoir toutes ces écritures: L'inverse de l'inverse d'un nombre est ce nombre: L'inverse de l'inverse d'une fraction est cette fraction:
Nombre décimal	L'inverse d'un nombre décimal est naturellement égal à 1 divisé par le nombre: On peut écrire le nombre décimal sous forme de fraction et prendre son inverse: Il n'est pas toujours possible de former une fraction équivalente. Exemple avec le nombre Pi:
Racines	La même règle s'applique aux racines, par contre, on souhaite souvent ne pas avoir de radicaux au dénominateur:

Calculatrice

Sur une calculatrice, on obtient l'inverse avec la touche 1/x ou la touche x^-1. Sur la calculatrice intégrée à Windows 10, la touche 1/x est révélée après avoir appuyé sur la flèche d'inversion () Voir Illustration

Somme des inverses et carrés
Deux nombres a et b. Prouver que N est supérieur ou égal à 4 (le carré de la quantité de nombres)		Propriété utilisée: la moyenne arithmétique est supérieure ou égale à la moyenne géométrique. En revenant à N:
Avec trois nombres		Comparaison des moyennes En revenant à N:
Avec quatre nombres		Le développement de la première ligne donne 4 + 12 termes = 16 = 4² (12 = 4 fois 3 cas de dénominateurs). Avec cinq nombres on aurait 5 + 20 termes = 25 = 5² Etc.
Théorème Généralisation à n nombres
Exemples

Voir Identités remarquables

Énigme

Si a + b + c + d = 16, trouvez la valeur minimale de 1/a + 1/b + 1/c + 1/d.

Selon le théorème précédent:

La valeur minimale recherchée est 1.

Elle est atteinte uniquement pour a = b = c = d = 4. Dans tous les autres cas, N est plus grand que 16. Exemple a = 3, b = c = 4 et d = 5, alors N = 1,0333…

Voir Énigmes – Index

Anglais	The reciprocal of a number is: 1 divided by the number. Also called the "Multiplicative Inverse"
En savoir plus	Voir suite en cliquant sur les mots de l'en-tête Voir aussi: Sommes des inverses de toutes natures Fractions égyptiennes Hyperbole Série harmonique – Somme des inverses Inversion (géométrie) Somme des inverses des carrés DicoMot

Cette page

http://villemin.gerard.free.fr/Referenc/Vocabula/GlosI/Inverse.htm