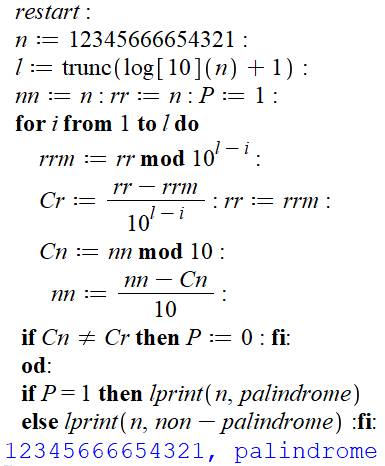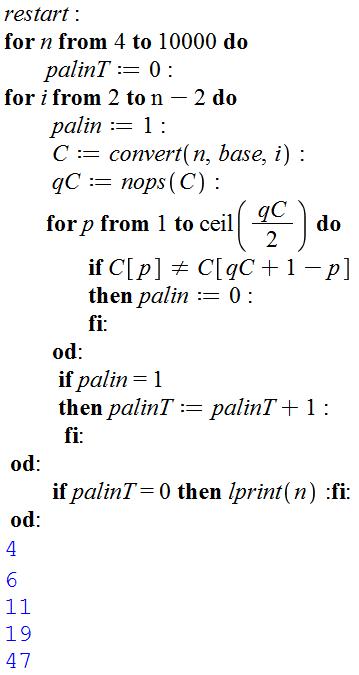|
|||||||||||||||||||||||||||||||||||
![]()
|
Palindromes numériques
|
|
|
||
|
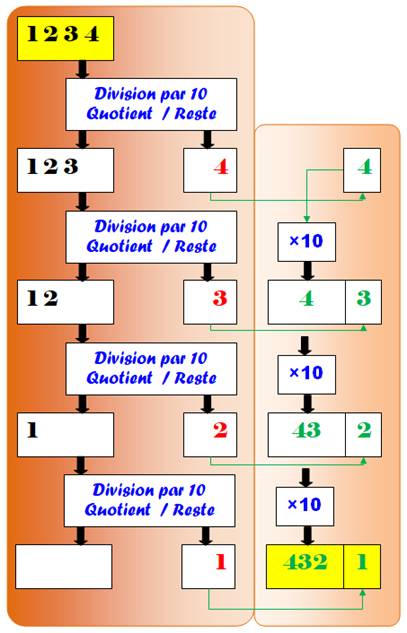
Algorithme
|
Implémentation Maple avec trace du
calcul
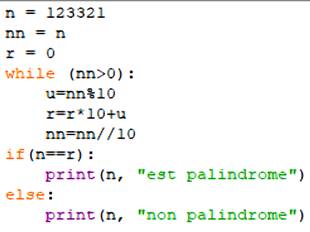
Implémentation Python
123321 est
palindrome |
|
Voir Programme
palindrome Python en deux lignes seulement (sans calcul)
![]()
Apprentissage de Maple avec les palindromes
Voir Apprentissage
de Python avec les palindromes
|
|
||
|
Observation Tester si
un nombre est un palindrome revient à comparer la liste des chiffres à sa
liste inversée. Si le logiciel
ne permet pas de disposer de la liste des chiffres, il faut opérer autrement.
C'est l'objet de ce premier programme. |
Ce premier programme de recherche des palindromes s'adresse aux
débutants en tant qu'exercice. Il est rare qu'un logiciel ne dispose pas des instructions facilitant
la tâche Voir le programme optimal avec liste |
|
|
Programme "bestial"
|
Commentaires Réinitialisation du logiciel et introduction manuelle d'un nombre n
que l'on place dans une mémoire de travail nn. Le nombre retourné sera
mémorisé en r. Formation du nombre n retourné Boucle qui tourne tant que nn, le nombre n amputé de l'unité à chaque
itération, n'a pas atteint 0. Le reste m de la division par 10 (mod 10) est placé en m et on calcule
la valeur du retourné r en ajoutant m à droite du retourné en cours de
formation. Vérification si n est palindrome Le nombre n et son retourné sont placés dans des mémoires de travail
nn et rr. Boucle avec nn comme précédemment. Si les deux chiffres en cour d'examen (unités de nn et de rr) sont
différent arrêt immédiat (break) et positionnement d'un indicateur P à zéro, indiquant que la recherche à échoué. Si en fin de boucle, l'indicateur P à résisté en restant à 1, c'est
que le nombre est palindrome. |
|
|
Programme avec comparaison directe
|
Principe Il est possible de raccourcir le programme en connaissant la longueur l du nombre. Elle
est calculée en prenant le log décimal de n. On pourra alors comparer les
chiffres par les deux bouts. Commentaires La boucle en i analyse les chiffres un à un jusqu'à "l" en
comparant le premier et le dernier. Il serait possible de limiter
l'exploration à la moitié de la longueur. Le nombre nn correspond à la recherche des chiffres par la droite,
alors que rr correspond à la recherche des chiffres par la gauche; un peu
plus difficile à calculer et nécessitant une mémorisation intermédiaire rrm. Si les chiffres extraits Cn et Cr sont différents, l'indicateur P est
mis à zéro. Si celui-ci reste à 1 au cours
de l'analyse, alors le nombre est palindrome. |
|
|
|
||
|
Programme
Listing restart: with(ListTools): n := 1122131; N := convert(n, base, 10); qN :=
nops(N); R := Reverse(N); t := evalb(N = R); if t = true then lprint(n,
palindrome) else lprint(n, non) end if: |
Principe On identifie les chiffres de n dans une liste, laquelle est inversée. Si les deux listes sont égales, le
nombre est palindrome. Commentaires Réinitialisation du logiciel et appel aux logiciels de manipulation de
liste. Introduction manuelle du nombre n. Conversion en base 10 qui délivre la liste des chiffres. La liste est inversée dans R. Les deux listes sont comparées avec evalb. Si elles sont identiques la variable logique t est vraie et, dans ce
cas, on indique que n est un palindrome. |
|
|
|
||
|
|
Principe Un nombre convertit en chaine de caractères et concaténé à son inverse. Ce programme
produit les palindromes pairs (à quantité paire de chiffres. Commentaires Réinitialisation et appel au logiciel de
traitement des listes (pour l'inversion). Conversion de n en chaine. Inversion de cette chaine Concaténation et retour à un nombre avec parse. |
|
|
|
Principe Ce programme construit tous les palindromes et les range dans une
liste ordonnée. Commentaires Avec c on crée
les palindromes comportant un chiffre médian. Les résultats sont placés dans l'ensemble(set) L
(liste ordonéée). |
|
|
|
||
|
Programme
|
Principe Prenez un nombre quelconque et ajoutez lui son retourné. Reproduisez
cette opération. Alors, apparaitra rapidement un palindrome, sauf pour les nombres
de Lychrel Commentaires Introduction manuelle d'un nombre (987). Lancement d'une boucle à 10 itérations (mettre plus si nécessaire,
notamment pour chercher des record de longueur de cycles). La variable kt
compte les itérations. Liste du nombre en N et de son retourné
en R. Lorsque N = R, alors le nombre atteint est palindrome. Celui-ci est
ajouté à la liste L. La boucle recommence en prenant n = n plus son retourné r. En fin de programme, on imprime la liste des valeurs successives de n
qui se termine par un palindrome après plus ou moins d'itérations. |
|
Voir Programmation – Index
![]()
Exercices
pour pratiquer la programmation
|
|
|
|
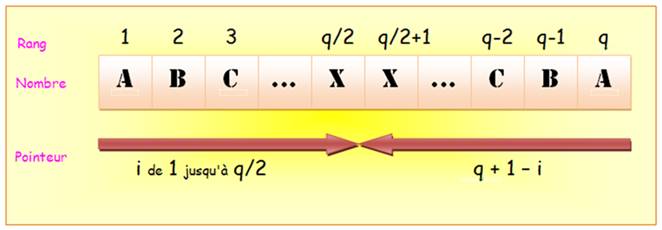
Prenons q pair
Exemple: 4 5 6
6 5 4
Si q est impair
Exemple: 4 5 6 7
6 5 4
|
|
|
|
> # Test si un nombre # est palindrome
N:=12321:
NC:=Chiffre(N):
q:=nops(NC): q2:=iquo(q,2):
Palin:= Vrai: for i from 1 to q2 do if NC[i]<>NC[q+1-i] then Palin:= Faux: fi: od: Palin;
|
|
La procédure Chiffre peut être
remplacée par la conversion en base 10 qui donne les chiffres.
Mais ce n'est plus la règle du jeu:
tout fabriquer!
|
|
||
|
|
> # Procédure Test si un nombre est palindrome Palin:= proc (n) local NC, q,q2,Palin,i;
NC:=Chiffre(n):
q:=nops(NC): q2:=iquo(q,2):
Palin:= Vrai: for i from 1 to q2 do if NC[i]<>NC[q+1-i] then Palin:= Faux fi: od:
lprint(n,Palin): end: > Palin(12321); Palin(123421); 12321, Vrai 123421, Faux |
|
|
|
||
|
Non seulement,
il y a 19 carrés palindromes jusqu'à n = 10 000, mais dix d'entre eux sont
doublement palindrome comme, par exemple, 11² = 121 ou encore 121² = 14641. |
> # Procédure Test si un nombre est palindrome Palin:= proc (n) local NC, q,q2,Palin,i;
NC:=Chiffre(n):
q:=nops(NC): q2:=iquo(q,2):
Palin:=
1: for i from 1 to q2 do if NC[i]<>NC[q+1-i] then Palin:= 0 fi: od: return(Palin): end: > #recherche
de carrés palindromes for i from 1 to 10000 do n:=i*i: T:=Palin(n): if T=1 then lprint(i,n): fi: od: 1, 1 2, 4 3, 9 11, 121 22, 484 26, 676 101, 10201 111, 12321 121, 14641 202, 40804 212, 44944 264, 69696 307, 94249 836, 698896 1001, 1002001 1111, 1234321 2002, 4008004 2285, 5221225 2636, 6948496 |
|
|
|
> #recherche
de cubes palindromes for
i from 1 to 10000 do n:=i*i*i: T:=Palin(n): if T=1 then lprint(i,n): fi: od: 1, 1 2, 8 7, 343 11, 1331 101, 1030301 111, 1367631 1001, 1003003001 2201,
10662526601 |
|
|
|
![]()
Bonus
|
|
||
|
Un nombre
strictement non palindrome
est non palindrome dans toutes les bases de 2 à n – 2. |
||
|
|
Initialisation
(remise à zéro de toutes les mémoires). Recherche
pour les nombres n de 4 à 10 000. L'indicateur
palinT à zéro indique qu'il n'y a
pas de palindrome pour n. Mis à 0 au
départ. Boucle
sur toutes les bases i de 2 à n –
2. L'indicateur
palin est à 1, supposant que le
nombre n dans la base i est un palindrome. C reçoit
le nombre n convertit dans la base i
et qC compte la quantité de
chiffres. Boucle de
vérification si ce nombre converti est un palindrome. S'il existe deux
chiffres symétriques non égaux, alors le nombre n'est pas palindrome et palin
est descendu à 0. Si le
nombre converti résiste, c'est qu'il est bien palindrome (palin = 1), alors on incrémente le
compteur de palindrome palinT. Si aucun
palindrome n'a été rencontré durant l'exploration des nombres convertis (palinT = 0), alors imprimer le nombre
n qui est bien un strictement non
palindrome. En bleu,
le début de l'impression lors de l'exécution du programme. |
|
![]()
|
Retour |
|
|
Suite |
|
|
Voir |
|
|
Cette page |
![]()
Programmes complets: les
procédures CHIFFRES et PALINDROME;
et le programme de
recherche des carrés palindromes
|
# Tous les programmes nécessaires
pour tester les carrés palindromes # Procédure CHIFFRE Chiffre:=proc(n) local C,nn, q, i,R:
nn:=n:
C:=[]:
while nn>0 do
C:=[op(C),irem(nn,10)];
nn:= iquo(nn,10): od:
q:=nops(C):R:=[]: for
i from 1 to q do
R:=[op(R),C[q-i+1]]
od: return (R): end: # Procédure PALINDROME Palin:=
proc (n) local NC, q,q2,Palin,i; NC:=Chiffre(n): q:=nops(NC): q2:=iquo(q,2): Palin:=
1:
for i from 1 to q2 do
if NC[i]<>NC[q+1-i]
then Palin:= 0
fi:
od: return(Palin): end: #recherche
de carrés palindromes for i from 1 to 100000 do
n:=i*i:
T:=Palin(n):
if T=1 then
lprint(i,n):
fi: od: 1, 1 2, 4 3, 9 11, 121 22, 484 26, 676 101, 10201 111, 12321 121, 14641 202, 40804 212, 44944 264, 69696 307, 94249 836, 698896 1001, 1002001 1111, 1234321 2002, 4008004 2285, 5221225 2636, 6948496 10001, 100020001 10101, 102030201 10201, 104060401 11011, 121242121 11111, 123454321 11211, 125686521 20002, 400080004 20102, 404090404 22865, 522808225 24846, 617323716 30693, 942060249 |
Pour copier ce
programme dans Mapple:
Sélectionner ce texte. Faites Ctrl C pour coller le texte dans le presse-papier.
Pointez l'endroit où vous voulez placer ce texte. Faites Ctrl V pour verser le contenu du presse-papier.
![]()
![]()