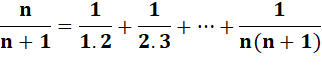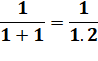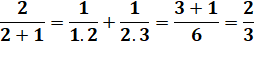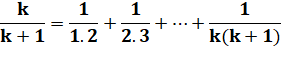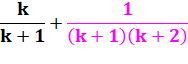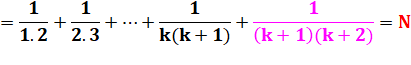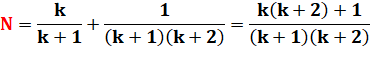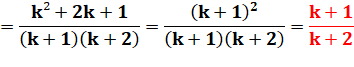NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 03/05/2019 Orientation générale  DicoMot Math Atlas Références M'écrire Barre de recherche DicoCulture Index alphabétique
	Forme des nombres
Débutants Général	Consécutifs			Glossaire Général
INDEX Formes et motifs	Index	Aperçu	Somme	Produit
		Produit-Carré
		Sommaire de cette page >>> Deux nombres consécutifs (ou jumeaux) >>> Florilège >>> Cinq consécutifs >>> Sommes simples >>> Produits simples >>> Division de consécutifs

NOMBRES CONSÉCUTIFS

Curiosités avec les chiffres consécutifs, comme:

12 = 3 x 4 (4 consécutifs)

12 = 3 + 4 + 5 (5 consécutifs)

Propriétés des nombres consécutifs, comme:

Le produit de 3 nombres consécutifs est divisible par 6, au moins

Le PGCD de deux nombres consécutifs est égal à 1
(aucun diviseur commun)

Deux nombres consécutifs (ou "jumeaux")
Deux nombres qui se suivent (n et n + 1).	(9, 10), (100, 101), (123456, 123457)
L'un d'eux est pair et l'autre impair. Le produit est divisible par 2.	9 x 10 = 90 = 2 x 45
Un des deux, au plus, est premier (sauf pour (2, 3)	( 9, 10) => deux composés (10, 11) => 11 est premier
La somme est impaire: S = 2n + 1 Si S est connu, on retrouve le nombre de tête: n = (S – 1) / 2	9 + 10 = 19 S = 101 => n = 100/2 = 50
Si la somme de deux nombres consécutifs (x – 3 et x – 4) vaut 13, quelle est la valeur de x	(x – 3) + (x – 4) = 13 2x = 20 x = 10
Le produit est pair: P = 2k (2k + 1) = 2 (2k² + k) Si P est connu, on retrouve les nombres en calculant la racine carrée: P = n² + n et en vérifiant la cohérence des unités.	P = 20 306 Racine: 142,5 Si 142 est bon, avec 143 le produit des unités convient. Solutions (142 et 143) ou (-142 et -143)
La somme de cinq nombres consécutifs est 50, quels sont ces nombres ?	Le choix de l'inconnu facilite le calcul: (n-2) + (n-1) + n + (n+1) + (n+2) = 5n = 50 Le nombre central est 10 Les nombres: 8, 9, 10, 11, 12
Est-ce que la somme de sept nombres consécutifs peut valoir 130 ?	(n-3) + (n-2) + (n-1) + n + (n+1) + (n+2) + (n+3) = 7n Or, 130 n'est pas divisible par 7.

FLORILÈGE – Belles formules

1 + 2 = 3 : forme triviale. Voir Trois consécutifs.

Formes simples:

6	= 1 / 2 ( 3 x 4 )	4 consécutifs	Dans l'ordre
56	= 7 x 8	4 consécutifs

12	= 3 x 4	4 consécutifs
12	= 3 + 4 + 5	5 consécutifs	12 et son retourné en 6 consécutifs
21	= 6 + 7 + 8	5 différents

Suite régulière de nombres

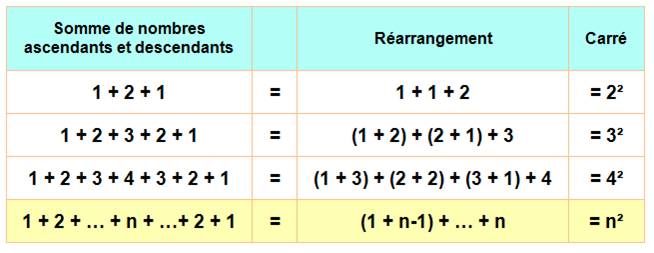
Voir Nombres carrés

La somme de la suite ascendante descendante est égale

au carré du nombre le plus grand

Voir Nombres carrés / Application de cette propriété

Formes en puissance

3² + 4² = 5² 3^3 + 4^3 + 5^3 = 6^3 (1 + 2 + 3)^2 = 1^3 + 2^3 + 3^3 (1 + 2 + 3 + 4 )^2 = 1^3 + 2^3 + 3^3 + 4^3

= 25 = 216 = 36 = 100

Voir Triplets de Pythagore / Somme au carré égale cube

Sommes et différences

1 + 2 2 + 3 3 + 4 4 + 5 …	= 2² – 1² = 3² – 2² = 4² – 3² = 5² – 4²
Somme de deux consécutifs	= Différence de leur carré

Impairs et puissances d'un nombre

1 + 3 + 5 = 9 = 3^2 7 + 9 + 11 = 27 = 3^3

Sommes de 6 nombres impairs qui donnent les puissances du nombre 3

Et la perfection …

1 x 2 x 3 =	6	Nombre parfait
4 x 5 x 6 =	120	Nombre triparfait
7 x 8 x 9 =	504 = 220 + 284	Somme d'une paire amiable

Cubes consécutifs

1	=	1^3	=	1
8	=	2^3	=	3 + 5
27	=	3^3	=	7 + 9 + 11
64	=	4^3	=	13 + 15 + 17 + 19
125	=	5^3	=	21 + 23 + 25 + 27 + 29
216	=	6^3	=	31 + 33 + 35 + 37 + 39 + 41
343	=	7^3	=	43 + 45 + 47 + 49 + 51 + 53 + 55
		…

Voir Cubes somme d'impairs

Cinq consécutifs

Trouvez cinq nombres consécutifs dont la somme est 100.

Formellement cette somme s'écrit:

n + (n+1) + (n+2) + (n+3) + (n+4) = 5n + 10

En formant l'égalité:

5 n + 10 = 100 et 5n = 90 soit n = 18

Voir Nombres triangulaires comme 1+2+3+4 = 10 / Partition avec des consécutifs

SOMMES SIMPLES

Motifs

12 =	3 + 4 + 5
	6 + 7 + 8	= 21

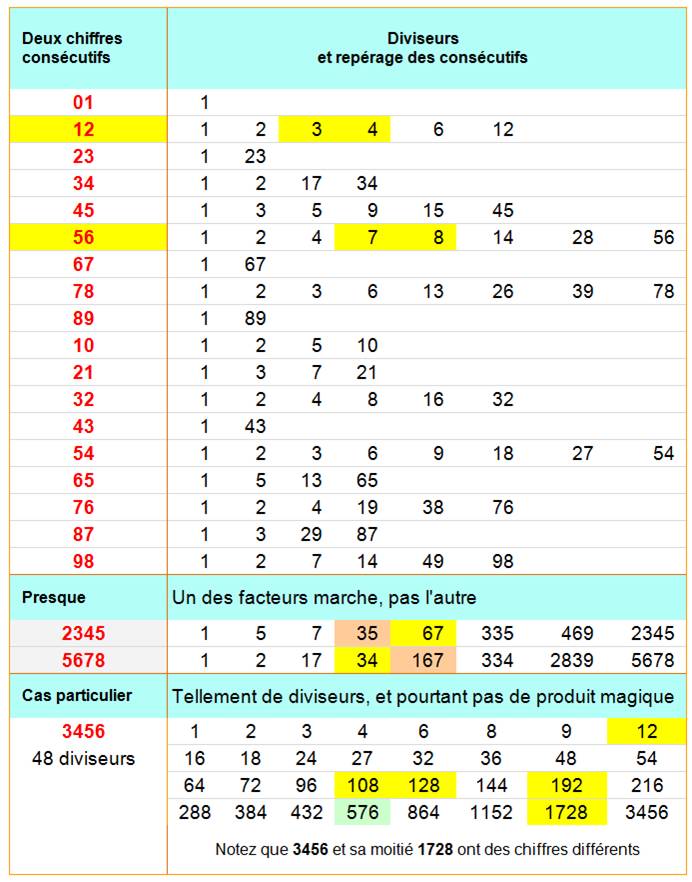
Autres, presque …

34	= 7 + 8 + 9 + 10	Somme de nombres consécutifs Chiffres différents
45	= 7 + 8 + 9 + 10 + 11	Somme de nombres consécutifs Chiffres non différents (le 1 est répété)

Ce genre de motifs trouvés pour 12 et 21 sont exceptionnels

Suite sans fin avec carrés

				1 +	2	=	3
			4 +	5 +	6	=	7	+ 8
		9 +	10 +	11+	12	=	13	+ 14	15
	16 +	17 +	18 +	19 +	20	=	21	+ 22	+ 23	+ 24
25 +	26 +	27 +	28 +	29 +	30	=	31 +	32 +	33 +	34 +	35
Etc.	Jusqu'à l'infini

À noter que le départ de chaque ligne est un carré, comme 25

Normal:

Deuxième ligne, en comparant les nombres de chaque côté de l'égalité:
de 5 à 7 il faut 2: de 6 à 8 il faut 2; soit un écart total de 2 x 2 = 2²

Troisième ligne: l'écart de 9 est obtenu avec trois fois une différence de 3 (10 à 13, 11 à 14 et 12 à 15)

Nous venons de constater une propriété commune à tous les carrés:

r² = n = – (n+1 + n+2 + … n+r) + (n+r+1 + n+r+2 + … n+r+r)

Exemples

5² = 25 = – (26 + 27 + 28 + 28 + 30) + (31 + 32 + 33 + 34 + 35)

PRODUITS SIMPLES

Huit chiffres consécutifs

12
	= 3 x 4
		56
			= 7 x 8

Motifs avec la suite des huit chiffres consécutifs.

Exploration

Division de consécutifs
Prouvez que:
Vraie pour n = 1 et 2.
Supposons que cette identité soit vraie pour n = k.
Ajoutons le terme suivant de chaque côté.
Le premier membre est égal au premier membre de notre égalité pour k+1.
Nous venons de montrer que la formule est vraie pour k+1 si elle est vraie pour k.	Par induction, la formule est vraie pour tout n.

Suite	Nombres consécutifs – Index Produit de consécutifs = carré ?
Voir	0,5 en chiffres 100 en chiffres Carré latin pannumérique Carré pannumérique Carrés et consécutifs Carrés Pannumériques Chiffres en miroir Concaténation et carrés Croix pannumérique Faire N avec k chiffres identiques Jeux (Index) Nombre têtu Nombres à motifs – Index Opérations – Glossaire Somme de 1 à 100 Sommes dans figures Soustraction Suite 0,1234…. Suite 1234... Suite 1234… Triangle
DicoNombre	Nombre 12 Nombre 56 Nombre 2345 Nombre 3456
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Formes/Consecut.htm