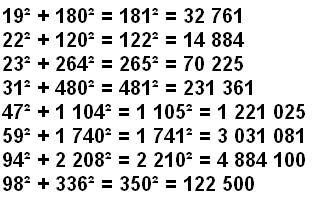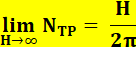|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
![]()
|
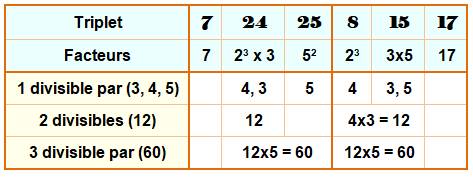
Triplets de Pythagore PROPRIÉTÉS
(3,
4, 5) est représentatif: 2
impairs et un pair divisibilité
par 3, 4 et 5 divisibilité
du produit par 60
(3,
4, 5) en le multipliant par 10 et 11 donne 30² +
40² = 50² 33² +
44² = 55² |
|
|
|||||||||||||||||||||
|
|||||||||||||||||||||
Autour
des triplets de Pythagore / Moyenne quadratique / Brève
430
|
|
|
|
Liste des triplets (a,b,c) tels que a² + b² = c² avec c
(3,4,5), (5,12,13), (6,8,10), (7,24,25), (8,15,17), (9,12,15), (9,40,41),
(10,24,26), (11,60,61), (12,16,20), (12,35,37), (13,84,85),
(14,48,50), (15,20,25), (15,36,39), (16,30,34), (16,63,65),
(18,24,30), (18,80,82), (20,21,29),
(20,48,52), (21,28,35), (21,72,75), (24,32,40), (24,45,51), (24,70,74),
(25,60,65), (27,36,45), (28,45,53),
(28,96,100), (30,40,50),
(30,72,78), (32,60,68), (33,44,55), (33,56,65),
(35,84,91), (36,48,60), (36,77,85),
(39,52,65), (39,80,89), (40,42,58),
(40,75,85), (42,56,70), (45,60,75), (48,55,73),
(48,64,80), (51,68,85), (54,72,90), (57,76,95), (60,63,87), (60,80,100), (65,72,97) Il y en a 50 pour c < 100 et 2 pour c= 100: total 52. Il y a 16 primitifs pour c < 100 |
|
Voir Illustration de la répartition / Comment les créer / Tables
/ Énigme du triangle inscrit
dans un rectangle
|
|
||||||||||||||
|
Si j'en ai un, je peux en construire une infinité d'autres
(a, b, c) <=> (k.a, k.b, k.c) car a² + b² = c² <=>
k².a² + k².b² = k².c²
Avec deux ou trois nombres
( a, b, c) = (u² –
v² , 2uv, u² + v²)
(A, B, C) = (a, b, c) M Différence de 1
n => ( n, ½ (n² – 1), ½ (n² + 1) )
Différence de 2
n, n + 1, n – 1 => M, N, O Qui
correspond au cas u = n et v = 1 de la formule générale.
Exemples de nombres avec b >> a:
|
||||||||||||||
Voir Triplets et nombres de Fibonacci
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Note: ½ Prouvé par
Lehmer (1900) Tableau: quantité
de triplets
(a, b, c) = (b - 1 , b , b + 1) b² - 2b +1 + b² = b² + 2b + 1 b²
= 4b b
= 0 ou b = 4 b
= 4 est l'unique solution
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
Si la différence
entre deux carrés est un carré, la somme et la différence des nombres est un
carré ou le double d'un carré. Exemple
|
|
|
|
|
|
Tout triplet
Triplets primitifs
PGCD(a,b) =
PGCD(a,c) = PGCD(b,c) = 1 Exemples de triplets primitifs 3
4 5 5 12 13 8 15 17 7 24 25 20 21
29 12 35
37 9 40 41 Formulation des principales propriétés du triplet primitif Si
(a,b,c) est un triplet primitif de Pythagore, alors :
|
|
|
Démonstration: a , b et c ne
sont pas tous impairs |
|
|
|
a = 2k + 1 b = 2n + 1 c = 2m + 1 |
|
|
(2k+1)² + (2n+1)² = (2m+1)² 4k² + 4k
+ 1 + 4n² + 4n + 1 = 4m² + 4m + 1 |
|
|
4.K |
|
Démonstration: a pair, b
impair et c impair
ou a impair, b pair et c impair |
|||
|
Contradiction
par rapport à l'hypothèse Donc
l'un des deux est impair. |
a et b aurait un diviseur
commun (2 ou 2.k) Or le triplet est primitif: a
et b n'ont pas de diviseur commun |
||
|
Le
carré de a divisé par 4 donne 1 pour reste. |
a = 2n+1 a² = 4n² + 4n + 1 a² = 1 mod 4 |
||
|
c² est un nombre
pair. |
a² = b² = 1 mod 4 c² = 1 + 1 mod 4 = 2 mod 4 |
||
|
c²
mod 4
donne 0 ou 1, jamais 2 |
c² = (2m)² = 4m²
= 0 mod 4 c² = 4m² + 4m + 1 = 1 mod 4 |
||
|
a et b ne
sont tous deux impairs. or
l'un est impair. |
a est pair b est impair |
ou |
a est impair b est pair |
|
c
selon
l'égalité. Selon
la parité de c. c pair donne. c impair donne. |
c² = a² + b² = 0 + 1 mod 2 =
1 mod 2 c² = (2n)² = 4n² = 0 mod2 c² = (2n+1)² = 1 mod 2 |
||
|
|
c est
impair |
||
|
Autre idée de la même démonstration |
|
|
L'équation
de Pythagore s'écrit => |
a = 2n+1 et b = 2m+1 a² + b² = c² (2n+1)² + (2m+1)² = c² 4n² + 4n + 1 + 4m² + 4m + 1 =
c² 4 (n² + n + m² + m) + 2 = c² |
|
c² pair implique c
pair. |
c = 2k |
|
Le
terme de droite est divisible par 4. Celui
de gauche ne l'est pas. Contradiction! Hypothèse
de départ fausse. |
4 (n² + n + m² + m) + 2 = 4k² a et b se sont pas impairs à la fois |
|
Démonstration: a ou b divisible par 4 |
|
|
Alors
b est impair, et
c est impair. |
a = 2k b = 2n+1 c = 2m+1 |
|
|
a² = c² - b² 4k² = 4m² + 4m + 1 - 4n² - 4n - 1 4k² = 4 (m² + m - n² - n) k² =
m² + m - n² - n k² = m (m+1) – n (n +1) |
|
Chacun
comporte deux nombres successifs dont l'un est pair |
m (m+1) = nombre pair n (n +1) = nombre
pair |
|
Cette
différence est paire. k² pair implique k
pair. |
k² = pair – pair k² = pair k = pair = 2h |
|
|
a = 2k = 2.2h = 4h |
|
|
a est divisible par 4 |
Merci à Francis Dalaudier
|
Démonstration: a, b ou c
divisible par 3 |
|
|
Le
reste de la division par 3 est 0, 1 ou 2. Le
reste de la division d'un carré est 0 ou 1. |
Divisible par 3 n = 0 mod 3 => n² = 0 x 0
= 0 mod 3 Non divisible par 3 n = 1 mod
3 => n² = 1 x 1 = 1 mod 3 n = 2 mod
3 => n² = 2 x 2 = 4 = 1 mod 3 |
|
Le
reste de la division par 3 et 1 ou 2. Le
reste de la division d'un carré est 1. |
|
|
Avec
la propriété des carrés => |
a² + b² = 1 + 1 = 2 mod 3 |
|
aucun
carré n'a 2 comme reste en le divisant par 3. |
n² |
|
L'un
des termes au moins est divisible par 3. |
a, b ou c divisible par 3 |
Voir Calcul avec les pairs et impairs
|
Démonstration: a . b . c
divisible par 60 donc par 3, par 4 et par 5 |
|
|
Supposons le triplet primitif,
sans perte de généralité. Les autres sont obtenus par multiplication de
ceux-ci. |
a, b, c Notons que le triplet célèbre (3,
4, 5) forme un produit déjà égal à 60. Et aussi que (3, 4 et 5) sont premiers entre eux. |
|
Si p et q sont générateurs
de triplets de Pythagore, alors |
a = 2pq b = p² – q² c = p² + q² |
|
Écriture du produit |
abc = (2pq) (p² – q²) (p² +
q²) = 2pq (p4 – q4) |
|
Divisibilité par 4 |
Or 2pq est divisible par 4, sauf si p et q sont tous
deux impairs, alors p² + q² est divisible par 2. abc est divisible par 4 |
|
Divisibilité par 3 Voir Congruences |
si p ou q si p et q et (p² – q²) abc est divisible par 3 |
|
Divisibilité par 5 |
si p ou q si p et q et (p4 – q4) abc est divisible par 5 |
|
|
||
|
Si x et y
sont impairs, alors N = x² + y² n'est jamais un carré. Notez: x² + y² = z² ne constitue un triplet de Pythagore que si l'un des
nombres x ou y est pair. |
Si x et y sont impairs: N = x² + y² = (2k + 1)² + (2h + 1) )² = 4(k² + k + h + h²) + 2 N est pair non divisible par 4. Si N = (2m + 1)² = 4m² + 4 m + 1 – Impossible Si N = (2m)² = 4m² – Impossible |
|
|
Si x et y
sont premiers avec 3, alors N = x² + y² n'est jamais un carré. Notez: x² + y² = z² ne constitue un triplet de Pythagore que si l'un des
nombres x ou y est divisible par 3. |
Forme des carrés: n = 3k => N = 9k² n = 3k + 1 => N = 9k² + k + 1 n = 3k + 2 => N = 9k² + 12k + 4 Donc jamais de la forme 3k + 2 Or x, comme y, sont premiers avec 3. x et y sont de la forme 3k + 1 ou 3k + 2. x² + y² = (3k + 1)² + (3h + 1)²
= 3K + 2 – Impossible x² + y² = (3k + 1)² + (3h + 2)²
= 3K + 5 – Impossible |
|
![]()
|
Suite |
|
|
Voir |
|
|
Sites |
|
|
Cette page |
http://villemin.gerard.free.fr/Wwwgvmm/Addition/TripProp.htm |
![]()