NOMBRES - Curiosités, théorie et usages Accueil DicoNombre Rubriques Nouveautés Édition du: 23/12/2022 Orientation générale  DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	Nombres Géométriques
Débutants Nombres géométriques	Nombres Triangulaires				Glossaire Nombres géométriques
INDEX Nombres géométriques Carré Penta Hexa Octa Déca	Définition	Propriétés	Particularités	Palindrome
	Caractérisation	Racines triangulaires		Centrés
		Relation de Fermat
		Sommaire de cette page >>> Approche >>> Nombres triangulaires >>> Triangulaires et carrés >>> Formule de calcul et remarques >>> Triangulaire en 6

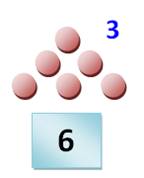
NOMBRES TRIANGLES
La suite des nombres consécutifs présente de l'intérêt: soit en sommes : les nombres triangulaires; soit en produits : les factorielles.	Conjecturé par Fermat en 1638 Démontré par Gauss 10 juillet 1796

Anglais: Triangular number

Devinette

Dans la salle du bar, on fête un anniversaire. Attentif, j'écoute et compte quarante-cinq tintements. Combien de personnes à cet anniversaire?

Solution

APPROCHE
Combien de pions faut-il empiler pour former un triangle équilatéral? Sur cet exemple: avec une base de 3, il en faut 2 puis 1 de plus; au total: 1 + 2 + 3 = 6 Un nombre triangulaire d'ordre n est la somme de tous les nombres consécutifs de 1 à n.

Nombres triangulaires
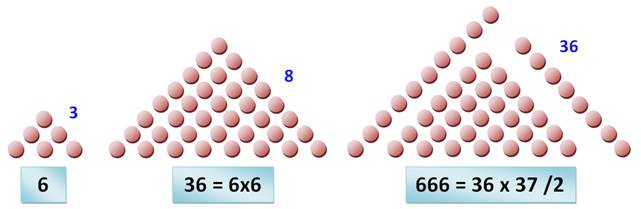
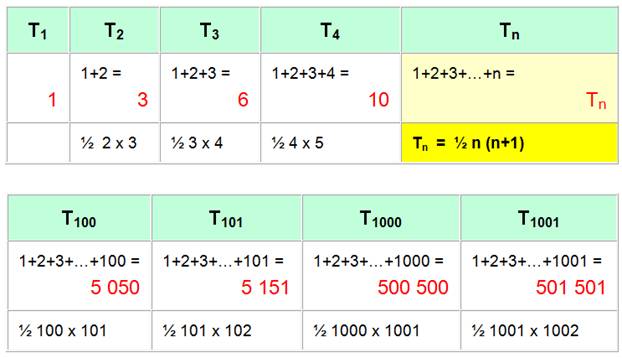
Les premiers en images Les premiers triangulaires en chiffres Voir Calcul de la somme des entiers Nombres triangulaires, carrés et produits des nombres successifs Voir Table / Suite originale

Les dix premiers nombres triangulaires

Triangulaires et carrés
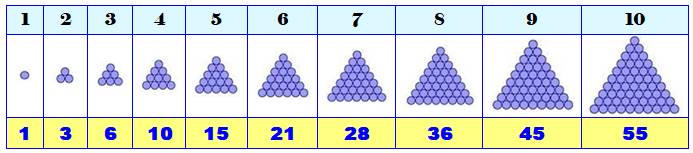
La somme de deux triangulaires successifs est un carré.

FORMULE DE CALCUL et remarques

Tn = ½ (n + 1) n = ½ (n^2 + n) Tn-1 = ½ (n - 1) n = ½ (n^2 - n) Voir Démonstration Les nombres en n (n + 1) sont appelés proniques. Parmi les deux nombres, l'un est pair et, le produit est pair. La moitié de ce nombre, un nombre triangulaire, est donc bien un nombre entier. Aucun nombre triangulaire, sauf 3, n'est premier En effet, parmi les deux facteurs n et n+1, l'un d'eux est pair (disons: 2k) et c'est lui qui est divisé par 2 pour donner: Dans l'un ou l'autre cas, Tn est un nombre composé à deux facteurs. Un triangulaire sur deux est hexagonal. La somme des triangulaires donne un nombre tétraédrique. La formule de calcul des tétraédraux est en n (n + 1) (n + 2). Un nombre triangulaire ne se termine jamais par 2, 4, 7, 9.

Curiosités

258 474 216 = ½ 22 736 x 22 737 = 636 x 637 x 638	Le plus grand triangulaire produit de trois nombres consécutifs.
T 26 62 = 354 4 453	Nombre triangulaire palindrome dont l'indice est lui-même palindrome (exemple).

Triangulaires et nombre 6
Présence du nombre 6 dans ces trois nombres triangulaires Notez que 6 x 6 x 6 = 6^3 = 216, terminé par un 6 comme toutes les puissances de 6.

Carrés en fonction des triangulaires
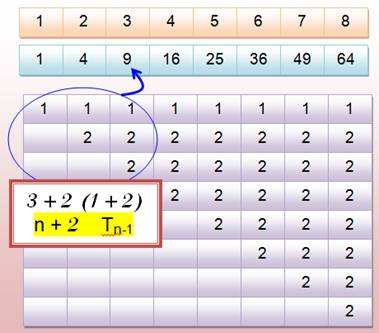
Voici une manière originale de présenter les carrés en fonction des nombres triangulaires. Elle résulte de la relation: n² = Tn – 1 + Tn Soit pour le suivant: n² = Tn + 1 + Tn – 1 + n n² = 2Tn + n Sur ce tableau, la valeur de n est présentée en horizontal par cumul de la valeur 1, le nombre triangulaire Tn est obtenu par cumul des valeurs dans le triangle, et le facteur 2 est obtenu en plaçant ce 2 dans chaque case du triangle.	Le carré de 3 est 9. Il est obtenu par la somme des nombres dans le triangle: 1 + 1 + 1 + 2 + 2 + 2. C'est, en fait, le nombre 3 additionné du nombre triangulaire précédent (le triangle des 2 est décalé d'un cran), doublé.

Devinette – Solution

Énigme

Dans la salle du bar, on fête un anniversaire. Attentif, j'écoute et compte quarante-cinq tintements. Combien de personnes à cet anniversaire?

Solution

Supposons quatre convives. Le premier trinque avec les trois autres. Le deuxième avec les deux qui restent. Le troisième avec le quatrième qui reste. Soit 3 + 2 + 1 = 6.

La quantité de tintements est un nombre triangulaire. Le nombre 45 est le neuvième. Il y a dix convives.

9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 45

Retour

Suite Nombres triangles	Propriétés (suite) Nomenclature Est-ce que N est triangulaire ? – Programme Nombre 271 – Six fois triangulaire + 1 TABLE – Triangulaires TABLE – Triangulaires centrés Nombres triangulaires et carré magique Nombre polygonaux centrés (traiteur paresseux) Nombres tétraédriques Nombres triangulaires et tétraédriques Nombres pentatopes Somme des nombres triangulaires
Voir Nombres géométriques	Introduction Valeurs Théorie Pythagore et nombres figurés
Voir aussi	Liste des noms de nombres Méthode de Newton Partition & Addition Raisonnement par récurrence Rubick's cube Somme des cubes des entiers Somme des triangulaires Sommes des entiers, carrés, inverses … Triplets primitifs jumeaux
DicoNombre	Nombre 6 Curiosité 351 Nombre 666
Cette page	http://villemin.gerard.free.fr/Wwwgvmm/Geometri/NbTrianB.htm