les nombres figurés ou géométriques

NOMBRES – Curiosités, Théorie et Usages Accueil DicoNombre Rubriques Nouveautés Édition du: 16/11/2022 Orientation générale DicoMot Math Atlas Actualités M'écrire Barre de recherche DicoCulture Index alphabétique Références Brèves de Maths
	COMPTER
Débutants Dénombrement	NOMBRES FIGURÉS				Glossaire Nombres figurés
INDEX Nombres figurés Géométrie Combinatoire Nombres	Débutants	Tour d'horizon	Introduction	Polygonaux
		Sommaire de cette page Présentation >>> Approche des nombres figurés >>> À quoi ça sert – Un exemple de relation Quelques nombres figurés simples >>> Nombres carrés >>> Les nombres premiers et les nombres composés Découvertes des relations entre nombres figurés >>> Les nombres triangulaires >>> Les triangulaires et les oblongs >>> Les oblongs et les pairs >>> Les carrés et les impairs >>> Bilan

NOMBRES FIGURÉS

ou géométriques

ou polygonaux

Ce site comporte de nombreux développements sur les nombres figurés. Ce sont les premiers éléments de réflexion historique sur la théorie des nombres. Ils sont également une source de découvertes et d'amusements. Les notions sont très facilement abordables.

Les premiers humains qui se mirent à compter, le faisaient avec l'aide d'entailles ou, ensuite, avec de petits cailloux.

La tentation est grande d'arranger les cailloux selon des figures géométriques.

C'est ce que firent les disciples de l'école de Pythagore.

Anglais: figurate numbers / polygonal numbers

Exemples

Approche des nombres figurés
Depuis l'Antiquité, les hommes ont été séduits par les figures géométriques. Il s'agissait de créer des dessins plus faciles à retenir ou à manipuler. Ce fut le cas pour les étoiles dans le ciel avec le dessin des constellations. Les mathématiciens de cette époque firent de même avec les nombres, en les arrangeant selon les figures géométriques les plus simples qu'ils connaissaient: le triangle, le carré, le pentagone, etc. 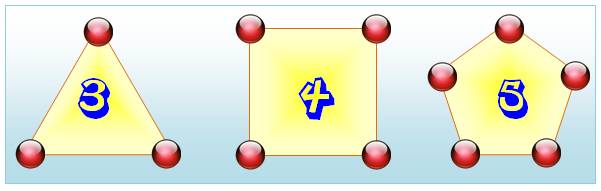Le nombre 3 est triangulaire; 4, un nombre carré et 5 un nombre pentagonal. Par défaut de former un dessin, le nombre 1 est triangulaire, carré ou pentagonal. Voir dans le DicoNombre: Nombre 3 / Nombre 4 / Nombre 5
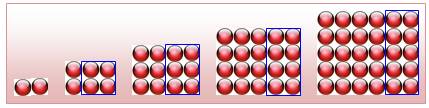
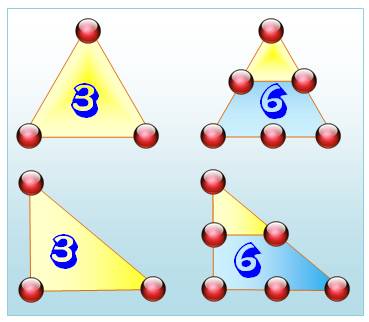
Pour commencer, il suffit de compter les sommets des figures géométriques simples appelées les polygones réguliers, dessins faits de traits de même longueur formant une jolie ligne brisée fermée. Passer au suivant consiste à poursuivre l'allure générale du dessin. Avec le triangle, la ligne suivante comporte 3 billes de plus et donne le nombre triangulaire suivant: 6. Pourquoi 3 billes de plus et non pas 2? Pour disposer du même nombre de billes sur chacun des côtés. Notez que le triangle initial est équilatéral (le plus "joli" des triangles). Cependant, les mêmes nombres triangulaires sont obtenus avec le triangle rectangle.	Les nombres triangulaires: 3 et 6, formés sur le triangle équilatéral ou sur le triangle rectangle.

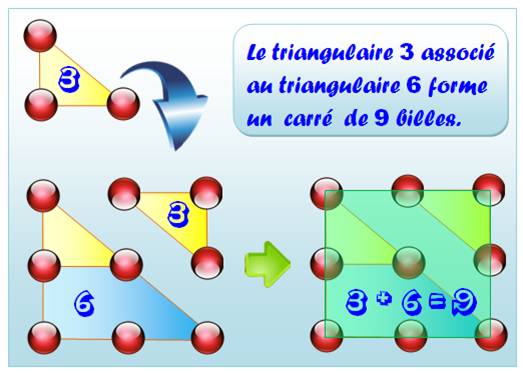
À quoi ça sert? – Un exemple de relation
Somme de triangulaires Prenons les deux nombres triangulaires successifs 3 et 6 et leur représentation avec le triangle rectangle. On forme une nouvelle figure en retournant le dessin du 3 sur le dessin du 6. La nouvelle figure est un carré égal à 9 qui est donc l'addition de 3 et 6. Propriété générale 3 + 6 = 9 = 3² T₂ + T₃ = C₃ Les suivants: 6 + 10 = 16 = 4² T₃ + T₄ = C₄ Et d'une manière générale: T_n-1 + T_n = C_n	Le deuxième triangulaire (T2) + le troisième triangulaire (T3) = le troisième carré (C3).
Sous forme résumée	Suite en Nombres triangulaires et carrés

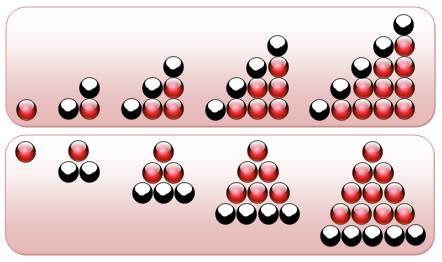
Quelques nombres figurés simples

Les nombres carrés
Nombres carrés Pour passer d'un carré au suivant on ajoute le nombre impair suivant. Ils sont de la forme qui consiste à prendre un nombre multiplié par lui-même, soit: n²	Les six premiers nombres carrés 1² 1 + 3 = 2² 4 + 5 = 3² 9 + 7 = 4² 16 + 9 = 5² 25 + 11 = 6² Suite en Nombres carrés
Nombres en L ou nombres impairs ou gnomons Si les nombres pairs peuvent se mettent en rang par 2, avec les nombres impairs, il y en a toujours un de plus. Ils sont de la forme: deux fois un nombre plus un, soit: 2n + 1	Les six premiers nombres impairs 1 3 = 2x1 + 1 5 = 2x2 + 1 7 = 2x3 + 1 9 = 2x4 + 1 11 = 2x5 + 1 Suite en Nombres pairs et impairs / Gnomons

Les nombres premiers et les nombres composés

Nombres rectangles

ou nombres composés

Finalement, un nombre rectangle est un nombre carré auquel on supprime un certain nombre de couches.

Ils sont de la forme: un nombre multiplié par un autre, soit:

n x m

Quelques exemples de nombres rectangulaires

2 x 3 = 6 3 x 4 = 12 3 x 5 = 15 5 x 6 = 30

Suite en Nombres composés / Tables de multiplication

Nombres presque-carrés ou proniques ou oblongs ou hétéromèques

Nombre rectangle issu d'un nombre carré avec une seule couche en moins.

Ils sont tous pairs et de la forme: un nombre multiplié par son successeur, soit

n (n + 1)

Les cinq premiers nombres proniques

1 x 2 = 2 2 x 3 = 6 3 x 4 = 12 4 x 5 = 20 5 x 6 = 30

Nombres linéaires ou nombres premiers

Nombres non-rectangles. Impossible de les mettre en rang par 2 ou 3 ou plus.

Contrairement aux autres, le passage d'un nombre au suivant ne semble pas suivre une logique. Les mathématiciens cherchent toujours. On les note:

Les cinq premiers nombres premiers

Suite en Nombres premiers / Barre magique des nombres premiers

Découverte des relations en nombres figurés

Les nombres triangulaires
Formation des nombres triangulaires Avec le triangle rectangle, on passe au suivant en ajoutant une hypoténuse (côté opposé à l'angle droit). Avec le triangle équilatéral, on ajoute une ligne à la base. Mais dans tous les cas, on ajoute autant de billes que le rang du nombre triangulaire. Pour calculer le cinquième nombre, on prend le quatrième et on ajoute 5.	Deux façons de construire les nombres triangulaires T1 = 1 T2 = 3 T3 = 6 T4 = 10 T5 = 15
Relations entres les nombres triangulaires Exemple: T4 = 10 qui se calcule en prenant T3 = 6 auquel on ajoute le rang 4: 6 + 4 = 10. Un nombre triangulaire de rang 4 est la somme de tous les nombres de 1 à 4. Un nombre triangulaire de rang n est la somme des entiers successifs de 1 à n. T_n = 1 + 2 + 3 + … + n Suite en Nombres triangulaires

Les triangulaires et les oblongs
Nombres triangulaires et nombres oblongs Un nombre oblong, produit de deux nombres successifs, est la somme de deux nombres triangulaires. Ou inversement, un nombre triangulaire est égal à la moitié d'un nombre oblong; il est aussi égal à la somme des nombre jusqu'à son rang.	Nombre oblong et identification de triangles Exemple avec le troisième: 3 x 4 = 2 T₃
Somme des entiers de 1 à n Un nombre triangulaire de rang n est la somme des entiers successifs de 1 à n, et il est égal au demi-produit de n par n + 1. T_n = 1 + 2 + 3 + … + n = 1/2 n (n + 1) Suite en Somme des entiers successifs

Les oblongs et les pairs
Nombres oblongs et nombres pairs Un nombre oblong est égal à son prédécesseur plus un nombre pair. En repartant du début, un nombre oblong est égal à la somme des nombres pairs successifs.	Formation des nombres oblongs 2 2 + 4 = 6 6 + 6 = 12 12 + 8 = 20 20 + 10 = 30 Exemple avec le quatrième: 2 + 4 + 6 + 8 = 4 x 5 = 20
Somme des nombres pairs de 2 à 2n La somme des nombres pairs de 2 à 2n est égale au nombre oblong n (n + 1). 2 + 4 + 6 + … + 2n = n (n +1) Suite en Somme des nombres pairs

Les carrés et les impairs
Carrés et impairs Un nombre carré est égal à son prédécesseur auquel est ajouté un nombre impair. En repartant du début, un carré est égal à la somme des nombres impairs successifs.	Exemple avec le troisième: 1 + 3 + 5 = 9 = 3²
Somme des nombres impairs de 1 à 2n – 1 La somme des nombres impairs de 1 à 2n+1 est égale au carré de n. 1 + 3 + 5 + … + (2n – 1) = n² Suite en Somme des nombres impairs

Bilan

Les nombres figurés, même les plus simples, sont riches de relations entre eux. Découvrez tout cela sur les pages de ce site: soit selon le type de nombres, soit selon les propriétés générales de ces nombres.

Dans le DicoNombre, vous retrouverez l'appartenance de chacun des nombres à sa représentation figurée jusqu'à n = 1000. Au-delà seuls les cas remarquables sont signalés.

Directions possibles:

Glossaire

Définition générale

et orientations

Introduction

Pour commencer

en douceur

Qui sont-ils ?

Valeurs, calcul, propriétés

Un par un

Nomenclature

La théorie

Les démonstrations

Suite	Nombre figurés - Développements Nombres figurés - Théorie
Retour	Combinatoire – Rubriques D'un coup d'œil
Voir	Cartes Compter – Index Compter les nombres Décade de Pythagore Dés Dominos Échecs Factorielle et ses cousines Grenouilles Jeux Nombre triangles et somme de nombres triangles Nombres géométriques - Formules et valeurs Nombres géométriques - Selon chaque type Nombres géométriques - Théorie Nombres pairs – Débutant Probabilités Pythagore Somme de premiers - Conjecture de Goldbach Somme de quatre carrés - Théorème de Lagrange Triangle de Pascal Types de Nombres – Débutant
Cette page	http://villemin.gerard.free.fr/Denombre/NbFigure.htm